题目内容
函数f(x)=sin(
x+θ)cos(
x+θ)(0<θ<π)在x=2时有最大值,则θ= ;将函数f(x)的图象向右平移
个单位得到函数g(x)的图象,则g(
)= .
| π |
| 2 |
| π |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质
分析:①利用三角恒等变换化简f(x),利用正弦函数的取得最大值求出θ的值;
②把f(x)的图象平移得出g(x)的解析式,从而求出g(
).
②把f(x)的图象平移得出g(x)的解析式,从而求出g(
| 2 |
| 3 |
解答:
解:①∵f(x)=sin(
x+θ)cos(
x+θ)
=
sin(πx+2θ),
∴f(2)=
sin(2π+2θ)
=
sin2θ=
;
又∵0<θ<π,
∴2θ=
,
解得θ=
;
②由①得,f(x)=
sin(πx+
)=
cosπx,
∴g(x)=
cos(π(x-
))=
cos(πx-
);
∴g(
)=
cos(
π-
)=
cos
=0.
故答案为:
,0.
| π |
| 2 |
| π |
| 2 |
=
| 1 |
| 2 |
∴f(2)=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
又∵0<θ<π,
∴2θ=
| π |
| 2 |
解得θ=
| π |
| 4 |
②由①得,f(x)=
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
∴g(x)=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
∴g(
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
故答案为:
| π |
| 4 |
点评:本题考查了三角函数的恒等变换以及三角函数求值问题,也考查了一定的计算能力,是基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
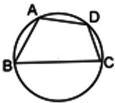 为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.
为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米. 如图△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是
如图△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是