题目内容
已知a，b，c是△ABC的三边，函数f（x）=
，则函数f（x）在R上（ ）
|
| A、单调递减 |
| B、单调递增 |
| C、无单调性 |
| D、单调性由a，b，c的值而定 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：首先，分x＜0和x≥0两种情形进行判断，然后，验证当x=0时，它们的函数值的大小．
解答：
解：∵x＜0，f（x）=-b（
）x+a，
-b＜0，
∴x＜0时为增函数，
当x≥0时，
∵e＞0，
∴f（x）在[0，+∞）为增函数，
且满足-b+a≤e，
故选D．
| 1 |
| e |
-b＜0，
∴x＜0时为增函数，
当x≥0时，
∵e＞0，
∴f（x）在[0，+∞）为增函数，
且满足-b+a≤e，
故选D．
点评：本题重点考查了分段函数的单调性，注意分界点处的函数值的比较，属于中档题．
练习册系列答案
相关题目
已知某几何体的三视图如图所示，其中侧视图为圆形，则该几何体的体积是（ ）
| A、π | B、2π | C、3π | D、6π |
| 5 |
| 2-i |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
若a，b，c∈C（C为复数集），则（a-b）2+（b-c）2=0是a=b=c的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
如图所示的程序框图，该算法的功能是（ ）
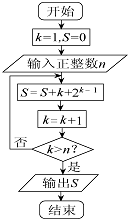
| A、计算（1+20）+（2+21）+（3+22）+…+（n+1+2n）的值 |
| B、计算（1+21）+（2+22）+（3+23）+…+（n+2n）的值 |
| C、计算（1+2+3+…+n）+（20+21+22+…+2n-1）的值 |
| D、计算[1+2+3+…+（n-1）]+（20+21+22+…+2n）的值 |
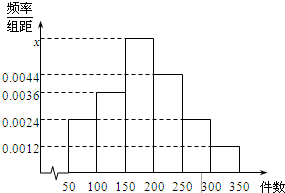从某工厂抽取50名工人进行调查，发现他们一天加工零件的个数在50至350个之间，现按生产的零件个数将他们分成六组，第一组[50，100），第二组[100，150），第三组[150，200），第四组[200，250），第五组[200，250），第六组[300，350），相应的样本频率分布直方图如图所示：