题目内容
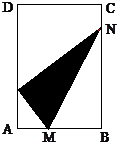 如图所示,在矩形纸片ABCD中,AB=6,AD=4
如图所示,在矩形纸片ABCD中,AB=6,AD=4| 3 |
A、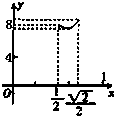 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD边E上,则△MNE≌△MNB,EM=BM,由∠MNB=θ,MN=l.由AB=6cm,我们可得EM+AM=6,然后将EM与BM分别用含θ的式子表示,代入即可得到l表示成θ的函数的解析式.进而得到函数y=F(x)的解析式,分析出函数的图象形状.
解答:
解:由题设,如图所示,△NBM≌△NEM,∠MNB=θ,MN=l,
∴∠AEM=90°-2θ,则MB=lsinθ,AM=l•sinθsin(90°-2θ),
由题设得:AM+MB=lsinθ+l•sinθsin(90°-2θ)=6,
从而得l=
=
=
,
∵sin∠MNB=sinθ=x,
∴y=F(x)=
又由BM=
≤6,BN=
≤4
得:x∈[
,
],
又由F′(x)=
,
当x∈[
,
]时,F′(x)≤0,此时F(x)为减函数,
当x∈[
,
]时,F′(x)≥0,此时F(x)为增函数,
比较四个答案中的图象,可知A符合,
故选:A.
∴∠AEM=90°-2θ,则MB=lsinθ,AM=l•sinθsin(90°-2θ),
由题设得:AM+MB=lsinθ+l•sinθsin(90°-2θ)=6,
从而得l=
| 6 |
| sinθ+sinθ•sin(90°-2θ) |
| 6 |
| sinθ+sinθ•cos2θ |
| 6 |
| sinθ+sinθ•(1-2sin2θ) |
∵sin∠MNB=sinθ=x,
∴y=F(x)=
| 6 |
| x+x•(1-2x2) |
又由BM=
| 3 |
| 1-x2 |
| 3 | ||
x
|
| 3 |
| 1 |
| 2 |
| ||
| 2 |
又由F′(x)=
| 12(3x2-1) |
| (-2x3+2x) |
当x∈[
| 1 |
| 2 |
| ||
| 3 |
当x∈[
| ||
| 3 |
| ||
| 2 |
比较四个答案中的图象,可知A符合,
故选:A.
点评:本题考查的知识点是函数的图象,函数的解析式,函数的定义域和函数的单调性,是函数图象和性质与导数的综合应用,综合性可,运算量大,属于难题.

练习册系列答案
相关题目
某同学从三个书店买四本不同的数学参考书,每个书店至少买一本书,则不同的购买方法有( )
| A、36种 | B、72种 |
| C、81种 | D、64种 |
对于定义在R上的奇函数f(x),满足f(x+
)=-f(x),则f(1)+f(2)+f(3)=( )
| 3 |
| 2 |
| A、0 | B、-1 | C、3 | D、2 |
若复数z满足z(4-3i)=(3+4i)2(i为虚数单位),则z=( )
| A、4+3i | B、4-3i |
| C、-4+3i | D、-4-3i |
已知点P(x,y)在直线2x+y+5=0上,那么x2+y2的最小值为( )
A、
| ||
B、2
| ||
| C、5 | ||
D、2
|
圆的半径变为原来的2倍,而弧长也增大到原来的2倍,则( )
| A、扇形的面积不变 |
| B、扇形的圆心角不变 |
| C、扇形的面积增大到原来的2倍 |
| D、扇形的圆心角增大到原来的2倍 |
已知a=log32,b=log25-log
3,c=lg5+
lg4,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、b>c>a |
| B、a>b>c |
| C、b>a>c |
| D、c>a>b |
已知复数z满足z=
(i为虚数单位),则z的共轭复数的虚部是( )
| 2i | ||
1+
|
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|