题目内容
对于定义在R上的奇函数f(x),满足f(x+
)=-f(x),则f(1)+f(2)+f(3)=( )
| 3 |
| 2 |
| A、0 | B、-1 | C、3 | D、2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由已知中f(x+
)=-f(x),可得函数的周期为3,再由奇函数的性质可得f(3)=,f(0)=0,f(2)=-f(1),代入计算可得.
| 3 |
| 2 |
解答:
解:∵f(x+
)=-f(x),
∴f(x+3)=-f(x+
)=f(x)
∴函数的周期为3,
又函数f(x)为R上的奇函数,
∴f(0)=0,
∴f(3)=(0+3)=f(0)=0,
∴f(2)=f(-1+3)=f(-1)=-f(1),
∴f(1)+f(2)+f(3)=f(1)-f(1)+0=0
故选:A
| 3 |
| 2 |
∴f(x+3)=-f(x+
| 3 |
| 2 |
∴函数的周期为3,
又函数f(x)为R上的奇函数,
∴f(0)=0,
∴f(3)=(0+3)=f(0)=0,
∴f(2)=f(-1+3)=f(-1)=-f(1),
∴f(1)+f(2)+f(3)=f(1)-f(1)+0=0
故选:A
点评:本题考查函数的周期性和奇偶性,属基础题.

练习册系列答案
相关题目
方程2x=cosx的解的个数为( )
| A、0 | B、1 | C、2 | D、无穷多个 |
函数f(x)=lg(4+3x-x2)的单调区间为( )
A、(-∞,
| ||
B、[
| ||
C、(-1,
| ||
D、[
|
命题“?x∈R,x2+x+3>0”的否定是( )
| A、?x∈R,x2+x+3≤0 |
| B、?x∈R,x2+x+3<0 |
| C、?x∈R,x2+x+3≤0 |
| D、?x∈R,x2+x+3<0 |
如图1放着一个长方体和一个圆柱,图2三幅图是它们的三视图,排列依次正确的是( )


| A、(1)正视图(2)侧视图(3)俯视图 |
| B、(1)正视图(2)俯视图(3)侧视图 |
| C、(1)俯视图(2)正视图(3)侧视图 |
| D、(1)俯视图(2)侧视图(3)正视图 |
如图的框图的功能是计算表达式1+2+3+…+10的值,则在①、②两处应填入( )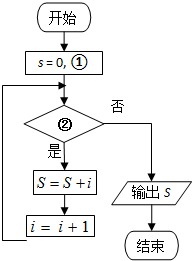

| A、i=0,i≤10 |
| B、i=0,i<10 |
| C、i=1,i≤10 |
| D、i=1,i<10 |
已知一组数据为0,-1,4,12,6,6,则这组数据的众数与中位数之和是( )
| A、10 | B、11 | C、13 | D、14 |
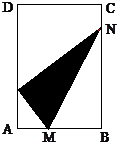 如图所示,在矩形纸片ABCD中,AB=6,AD=4
如图所示,在矩形纸片ABCD中,AB=6,AD=4