题目内容
已知点P(x,y)在直线2x+y+5=0上,那么x2+y2的最小值为( )
A、
| ||
B、2
| ||
| C、5 | ||
D、2
|
考点:点到直线的距离公式
专题:直线与圆
分析:x2+y2的最小值可看成直线2x+y+5=0上的点与原点连线长度的平方最小值,由点到直线的距离公式可得.
解答:
解:x2+y2的最小值可看成直线2x+y+5=0上的点与原点连线长度的平方最小值,
即为原点到该直线的距离平方d2,
由点到直线的距离公式易得d=
=
.
∴x2+y2的最小值为5,
故选:C
即为原点到该直线的距离平方d2,
由点到直线的距离公式易得d=
| |2×0+0+5| | ||
|
| 5 |
∴x2+y2的最小值为5,
故选:C
点评:本题考查点到直线的距离公式,转化是解决问题的关键,属基础题.

练习册系列答案
相关题目
如图是某程序框图,若执行后输出y的值为0,则输入x的值不能是( )


| A、0 | ||
B、
| ||
| C、2 | ||
| D、2010 |
命题“?x∈R,x2+x+3>0”的否定是( )
| A、?x∈R,x2+x+3≤0 |
| B、?x∈R,x2+x+3<0 |
| C、?x∈R,x2+x+3≤0 |
| D、?x∈R,x2+x+3<0 |
如图的框图的功能是计算表达式1+2+3+…+10的值,则在①、②两处应填入( )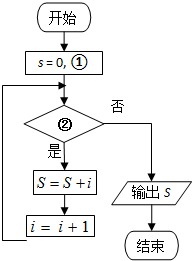

| A、i=0,i≤10 |
| B、i=0,i<10 |
| C、i=1,i≤10 |
| D、i=1,i<10 |
已知数据x1,x2,x3的中位数为k,众数为m,平均数为n,方差为p,则下列说法中,错误的是( )
| A、数据2x1,2x2,2x3的中位数为2k |
| B、数据2x1,2x2,2x3的众数为2m |
| C、数据2x1,2x2,2x3的平均数为2n |
| D、数据2x1,2x2,2x3的方差为2p |
函数f(x)=tanx-
在区间(-
,
)内的零点个数是( )
| 1 |
| x |
| π |
| 2 |
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
某校在一天的6节课中随机安排语文、数学、英语三门文化课和音乐、体育、美术三种艺术课各一节,则在课表上的相邻2节文化课之间至少间接一节艺术课的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
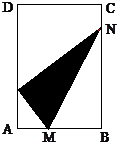 如图所示,在矩形纸片ABCD中,AB=6,AD=4
如图所示,在矩形纸片ABCD中,AB=6,AD=4