题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知
=
,且C=
.
(Ⅰ)求角A,B的大小;
(Ⅱ)设函数f(x)=sin(2x+A)-sin2x+cos2x,求函数f(x)的最小正周期及最小值.
| cosA |
| cosB |
| b |
| a |
| 2π |
| 3 |
(Ⅰ)求角A,B的大小;
(Ⅱ)设函数f(x)=sin(2x+A)-sin2x+cos2x,求函数f(x)的最小正周期及最小值.
考点:正弦定理的应用,三角函数的最值
专题:三角函数的求值,三角函数的图像与性质,解三角形
分析:(Ⅰ)由已知及正弦定理可得sin2A=sin2B,有A=B,由已知角C=
,即可求出A,B的大小;
(Ⅱ)化简函数解析式可得f(x)=
sin(2x+
),即可求函数f(x)的最小正周期及最小值.
| 2π |
| 3 |
(Ⅱ)化简函数解析式可得f(x)=
| 3 |
| π |
| 3 |
解答:
解:(Ⅰ)∵
=
,由正弦定理得
=
,
即sin2A=sin2B,
∴A=B或A+B=
(舍去),
又∵C=
,
∴A=B=
.
(Ⅱ)f(x)=sin(2x+A)-sin2x+cos2x=sin(2x+
)+cos2x
=sin2xcos
+cos2xsin
+cos2x
=
sin2x+
cos2x=
sin(2x+
),
∴最小正周期T=
=π,最小值为-
.
| cosA |
| cosB |
| b |
| a |
| cosA |
| cosB |
| sinB |
| sinA |
即sin2A=sin2B,
∴A=B或A+B=
| π |
| 2 |
又∵C=
| 2π |
| 3 |
∴A=B=
| π |
| 6 |
(Ⅱ)f(x)=sin(2x+A)-sin2x+cos2x=sin(2x+
| π |
| 6 |
=sin2xcos
| π |
| 6 |
| π |
| 6 |
=
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
∴最小正周期T=
| 2π |
| |ω| |
| 3 |
点评:本题主要考查了正弦定理的应用,三角函数的图象与性质,属于基础题.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差数列,a+c=2,则b的取值范围是( )
| A、[1,2) | ||
| B、(0,2] | ||
C、[1,
| ||
| D、[1,+∞) |
若变量x,y满足约束条件
,则z=2x+y的最大值是( )
|
| A、2 | B、4 | C、5 | D、6 |
函数y=ax-1+2(a>0,且a≠1)的图象恒过点的坐标为( )
| A、(2,2) |
| B、(2,4) |
| C、(1,2) |
| D、(1,3) |
如果tan(α+β)=
,tan(α-
)=
,那么tan(β+
)=( )
| 3 |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
如图,P、Q是线段AB的三等分点,若
=
,
=
,则
-
=( )
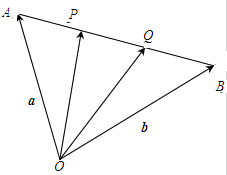
| OA |
| a |
| OB |
| b |
| OP |
| OQ |

A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
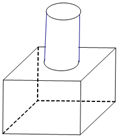 某机器零件是如图所示的几何体(实心),零件下面是边长为10cm的正方体,上面是底面直径为4cm,高为10cm的圆柱.
某机器零件是如图所示的几何体(实心),零件下面是边长为10cm的正方体,上面是底面直径为4cm,高为10cm的圆柱.