题目内容
(1)在公园游园活动中有一个射击游戏项目,某人参加该游戏,结果服从线性回归方程
=
x+a,其中x表示每组射击次数,y表示每组命中的平均环数,共射击10组后,样本的平均数据为
=10,
=8,求参数a.
(2)在公园游园活动另一个游戏项目:甲箱子里装有a(a为(1)中的结果)个白球和2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
①求在1次游戏中获奖的概率;
②求在两次游戏中,获奖次数记为X,求X的分布列及数学期望.
 |
| y |
| 1 |
| 2 |
. |
| x |
. |
| y |
(2)在公园游园活动另一个游戏项目:甲箱子里装有a(a为(1)中的结果)个白球和2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
①求在1次游戏中获奖的概率;
②求在两次游戏中,获奖次数记为X,求X的分布列及数学期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)把
=10,
=8分别代入回归方程
=
x+a,能求出a=3.
(2)(Ⅰ)(i)设“在一次游戏中摸出i个白球”为事件Ai(i=,0,1,2,3),设“在一次游戏中获奖”为事件B,则B=A2∪A3,由A2、A3互斥,能求出在1次游戏中获奖的概率.
(Ⅱ)由题意可知X的所有可能取值为0,1,2,由题意X~B(2,
),由此能求出X的分布列及数学期望.
. |
| x |
. |
| y |
 |
| y |
| 1 |
| 2 |
(2)(Ⅰ)(i)设“在一次游戏中摸出i个白球”为事件Ai(i=,0,1,2,3),设“在一次游戏中获奖”为事件B,则B=A2∪A3,由A2、A3互斥,能求出在1次游戏中获奖的概率.
(Ⅱ)由题意可知X的所有可能取值为0,1,2,由题意X~B(2,
| 7 |
| 10 |
解答:
解:(1)∵回归方程
=
x+a,其中x表示每组射击次数,y表示每组命中的平均环数,
共射击10组后,样本的平均数据为
=10,
=8,
∴8=
×10+a,解得a=3.
(2):(Ⅰ)(i)设“在一次游戏中摸出i个白球”为事件Ai(i=,0,1,2,3),
设“在一次游戏中获奖”为事件B,则B=A2∪A3,
又P(A2)=
•
+
•
=
,
P(A3)=
•
=
,
且A2、A3互斥,
所以P(B)=P(A2)+P(A3)=
+
=
.
(Ⅱ)由题意可知X的所有可能取值为0,1,2.由题意X~B(2,
),
P(X=0)=(1-
)2=
,
P(X=1)=C21
(1-
)=
,
P(X=2)=(
)2=
,
所以X的分布列是
X的数学期望E(X)=0×
+1×
+2×
=
.
 |
| y |
| 1 |
| 2 |
共射击10组后,样本的平均数据为
. |
| x |
. |
| y |
∴8=
| 1 |
| 2 |
(2):(Ⅰ)(i)设“在一次游戏中摸出i个白球”为事件Ai(i=,0,1,2,3),
设“在一次游戏中获奖”为事件B,则B=A2∪A3,
又P(A2)=
| ||
|
| ||
|
| ||||
|
| ||
|
| 1 |
| 2 |
P(A3)=
| ||
|
| ||
|
| 1 |
| 5 |
且A2、A3互斥,
所以P(B)=P(A2)+P(A3)=
| 1 |
| 2 |
| 1 |
| 5 |
| 7 |
| 10 |
(Ⅱ)由题意可知X的所有可能取值为0,1,2.由题意X~B(2,
| 7 |
| 10 |
P(X=0)=(1-
| 7 |
| 10 |
| 9 |
| 100 |
P(X=1)=C21
| 7 |
| 10 |
| 7 |
| 10 |
| 21 |
| 50 |
P(X=2)=(
| 7 |
| 10 |
| 49 |
| 100 |
所以X的分布列是
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 9 |
| 100 |
| 21 |
| 50 |
| 49 |
| 100 |
| 7 |
| 5 |
点评:本题考查回归直线方程的应用,考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
下列函数是以π为周期的偶函数的是( )
| A、y=tanx | ||
B、y=sin(x+
| ||
C、y=sin(2x+
| ||
D、y=cos(2x+
|
命题“事件A与事件B互斥”是命题“事件A与事件B对立”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
若正数a,b满足ab=a+b+8,则ab的取值范围是( )
| A、(0,16] |
| B、[4,16) |
| C、[4,16] |
| D、[16,+∞) |
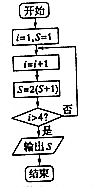 在如图所示的程序框图表示的算法中,输出的结果是
在如图所示的程序框图表示的算法中,输出的结果是