题目内容
19.已知直线kx+y-k=0与射线3x-4y+5=0(x≥-1)有交点,求实数k的取值范围.分析 根据题意,画出图形,结合图形,得出直线kx+y-k=0过定点M(1,0),
射线3x-4y+5=0(x≥-1)的端点是P(-1,$\frac{1}{2}$),由此得出直线与射线有交点时实数k的取值范围.
解答 解:直线kx+y-k=0可化为k(x-1)+y=0,
该直线恒过定点M(1,0),
又射线3x-4y+5=0(x≥-1)的端点P(-1,$\frac{1}{2}$),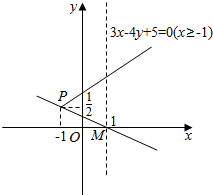
如图所示;
①当斜率小于0时:
把点P(-1,$\frac{1}{2}$)的坐标代入直线方程k(x-1)+y=0中,
解得k=$\frac{1}{4}$,∴-k≤-$\frac{1}{4}$,即k≥$\frac{1}{4}$时,有交点;
②当斜率大于0时:
要两直线有交点,则-k>$\frac{3}{4}$,即k<-$\frac{3}{4}$;
综上,直线kx+y-k=0与射线3x-4y+5=0(x≥-1)有交点时,
实数k的取值范围是k<-$\frac{3}{4}$或k≥$\frac{1}{4}$.
点评 本题考查了两条直线的交点问题,也考查了数形结合的应用问题,是基础题目.

练习册系列答案
相关题目
7.已知sinα<0且tanα>0,则角α所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.已知函数f(x)=-x2-2x,g(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{x+\frac{1}{4x},x>0}\end{array}\right.$,若函数y=g(f(x))-a有4个零点,则实数a的取值范围是( )
| A. | (0,1] | B. | ($\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,$\frac{5}{4}$) | D. | [1,$\frac{5}{4}$) |
 如图,A、B、C为函数y=log2x图象上的三点,它们的横坐标为t,t+2,t+4,(其中t≥1),AA1、BB1、CC1与x轴垂直,垂足为A1、B1、C1.
如图,A、B、C为函数y=log2x图象上的三点,它们的横坐标为t,t+2,t+4,(其中t≥1),AA1、BB1、CC1与x轴垂直,垂足为A1、B1、C1.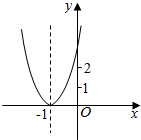 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )