题目内容
13.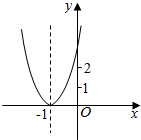 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据已知中函数的图象,分析函数的性质,并逐一分析四个结论的真假,可得答案.
解答 解:由已知中二次函数y=ax2+bx+c+2的图象,可得:a>0,b>0,c+2>2,即c>0,
故abc>0成立,故①错误;
由函数图象与x轴有且仅有一个交点,可得△=b2-4ac=0,故②正确;
二次函数y=ax2+bx+c+2的顶点式方程为:y=a(x+1)2,
当x=0时,y=a>2,故③正确;
当x=-2时,y=4a-2b+c>0,故④正确;
综上正确结论的个数是3个,
故选:C.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
1.某几何体的一条棱长为3,在该几何体的正视图中,这条棱的投影长为2的线段,在该几何体的侧视图和俯视图中,这条棱长的投影长分别是a和b的线段,则a+b的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{7}$ | C. | 4 | D. | 2$\sqrt{6}$ |
2.若a=0.32,b=log20.3,c=20.3,则a,b,c大小关系正确的是( )
| A. | c>a>b | B. | a>b>c | C. | c>b>a | D. | c>b>a |
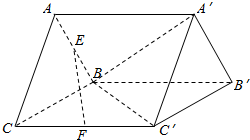 已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.