题目内容
4.设满足y≥|x-a|的点(x,y)的集合为A,满足y≤-|x|+b的点(x,y)的集合为B,其中a,b为正数.(1)用平面区域表示出集合A、B,并探求a,b的关系式,使A∩B≠∅.
(2)在(1)的条件下,求A∩B表示区域的面积.
分析 (1)在同一坐标系内画出y≥|x-a|、y≤-|x|+b所表示的平面区域,数形结合可得使A∩B≠∅的a,b之间的关系;
(2)由(1)知,A∩B所表示的图形为矩形ACBD,求出矩形面积即可.
解答 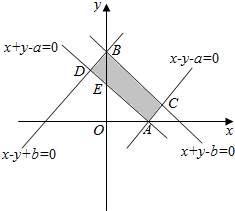 解:(1)不等式y≥|x-a|可化为$\left\{\begin{array}{l}{x-y-a≤0}\\{x≥a}\end{array}\right.$或$\left\{\begin{array}{l}{x+y-a≥0}\\{x<a}\end{array}\right.$,画出它所表示的平面区域如图所示,
解:(1)不等式y≥|x-a|可化为$\left\{\begin{array}{l}{x-y-a≤0}\\{x≥a}\end{array}\right.$或$\left\{\begin{array}{l}{x+y-a≥0}\\{x<a}\end{array}\right.$,画出它所表示的平面区域如图所示,
不等式y≤-|x|+b可化为$\left\{\begin{array}{l}{x-y-b≤0}\\{x≥0}\end{array}\right.$或$\left\{\begin{array}{l}{x-y+b≥0}\\{x<0}\end{array}\right.$,
将其表示的平面区域与A表示的平面区域画在同一坐标系中,
如图所示,要使A∩B≠∅,只要b≥a;
(2)由(1)知,A∩B所表示的图形为矩形ACBD,
BE=b-a,在Rt△BDE中,∠DBE=45°,
∴BD=$\frac{\sqrt{2}}{2}$(b-a),
又AD=AE+DE=$\sqrt{2}$a+$\frac{\sqrt{2}}{2}$(b-a)=$\frac{\sqrt{2}}{2}$(b+a),
∴矩形面积S=BD•AD=$\frac{1}{2}({b}^{2}-{a}^{2})$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,正确作出图形是解答该题的关键,是中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
14.若∠A=22°,∠B=23°,则(1+tanA)(1+tanB)的值是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1+$\sqrt{2}$ | D. | 2(tanA+tanB) |
9.如果关于x的不等式ax2+bx+c<0的解集是{x|x<-2或x>-1},那么关于x的不等式cx2-bx+a>0的解集为( )
| A. | (-1,$\frac{1}{2}$) | B. | (-1,-$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (-$\frac{1}{2}$,1) |
1.某几何体的一条棱长为3,在该几何体的正视图中,这条棱的投影长为2的线段,在该几何体的侧视图和俯视图中,这条棱长的投影长分别是a和b的线段,则a+b的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{7}$ | C. | 4 | D. | 2$\sqrt{6}$ |