题目内容
14.关于x的不等式$|{\begin{array}{l}x&1\\ a&{x-2}\end{array}}|>0$的解集为R,则实数a的取值范围为(-∞,-1).分析 由二阶行列式展开法则得x2-2x-a>0的解集为a,由此能求出实数a的取值范围.
解答 解:∵$|{\begin{array}{l}x&1\\ a&{x-2}\end{array}}|>0$的解集为R,
∴x2-2x-a>0的解集为a,
∴△=4+4a<0,
解得a<-1,
∴实数a的取值范围为(-∞,-1).
故答案为:(-∞,-1).
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意二阶行列式展开法则的合理运用.

练习册系列答案
相关题目
2.若a=0.32,b=log20.3,c=20.3,则a,b,c大小关系正确的是( )
| A. | c>a>b | B. | a>b>c | C. | c>b>a | D. | c>b>a |
9.方程xlnx-2=0的解所在的区间是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
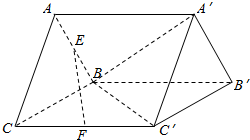 已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.