题目内容
9.(1)已知sin(π+α)=$\frac{1}{3}$,求sin(-3π+α)的值.(2)已知cos($\frac{π}{3}+α$)=-$\frac{1}{2}$,求cos($α-\frac{5π}{3}$)的值.
分析 由条件利用诱导公式,化简求得要求式子,可得结果.
解答 解:(1)∵sin(π+α)=-sinα=$\frac{1}{3}$,∴sinα=-$\frac{1}{3}$,∴sin(-3π+α)=sin(π+α)=-sinα.
(2)∵cos($\frac{π}{3}+α$)=-$\frac{1}{2}$,求cos($α-\frac{5π}{3}$)=cos(α+$\frac{π}{3}$)=-$\frac{1}{2}$.
点评 本题主要考查利用诱导公式求得要求式子的值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若∠A=22°,∠B=23°,则(1+tanA)(1+tanB)的值是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1+$\sqrt{2}$ | D. | 2(tanA+tanB) |
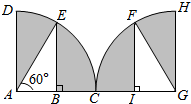 如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)
如图所示,两个四分之一圆面ACD和GCH交于点C点,AD=CH=10厘米,∠EAB=∠FGC=60°,EB与FI分别垂直于AC和GC,则阴影部分为85.28平方厘米.(π取3.14)