题目内容
若两个等差数列{an}和{bn}的前n项和分别是Sn和Tn，已知
=
，则
等于（ ）
| Sn |
| Tn |
| n |
| 2n+1 |
| a7 |
| b7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：等差数列的性质
专题：等差数列与等比数列
分析：利用等差数列的性质可知
=
，从而可得答案．
| a7 |
| b7 |
| S13 |
| T13 |
解答：
解：∵
=
，
∴
=
=
=
=
=
，
故选：C．
| Sn |
| Tn |
| n |
| 2n+1 |
∴
| a7 |
| b7 |
| 2a7 |
| 2b7 |
| ||
|
| S13 |
| T13 |
| 13 |
| 2×13+1 |
| 13 |
| 27 |
故选：C．
点评：本题考查等差数列的性质，得到
=
是关键，考查运算能力，属于中档题．
| a7 |
| b7 |
| S13 |
| T13 |
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知函数f（x）=cosxsinx，x∈R，则f（x）是（ ）
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
下列命题错误的是（ ）
| A、命题“若p则q”与命题“若￢q则￢p”互为逆否命题 |
| B、命题“?x∈R，x2-x＞0”的否定是“?x∈R，x2-x≤0” |
| C、命题“若a＜b，则am2＜bm2”的否命题为真 |
| D、命题“若b2=ac，则a，b，c成等比数列”的逆命题为假 |
设集合S={x|2x＞
}，T={x|-4≤x≤1}，则S∩T=（ ）
| 1 |
| 4 |
| A、[-4，+∞） |
| B、（-2，+∞） |
| C、[-4，1] |
| D、（-2，1] |
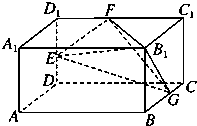如图，长方体AC1中，AB=2，BC=AA1=1．E、F、G分别为棱DD1、D1C1、BC的中点．