题目内容
4.若直线l被4x+y+6=0和3x-5y-6=0两条直线截得的线段的中点恰好是坐标原点,求直线l的方程.分析 截得的线段的中点恰好是坐标原点,直线l与4x+y+6=0和3x-5y-6=0的交点关于原点对称,交点适合两直线,联立方程,又直线过原点,因而消去常数可得所求直线方程.
解答 解:设所求直线l与已知两直线的交点分别是A、B,设A(x0,y0),
∵A、B关于原点对称,
∴B(-x0,-y0).
又∵A、B分别在两直线上,
∴$\left\{\begin{array}{l}{4{x}_{0}+{y}_{0}+6=0}\\{-3{x}_{0}+5{y}_{0}-6=0}\end{array}\right.$,解得x0+6y0=0,即点A在直线x+6y=0上,又直线x+6y=0过原点,
∴直线l的方程是x+6y=0.
点评 本题考查直线方程的求法,解题时要注意中点坐标公式的合理运用,本题解答比较有技巧,是基础题.

练习册系列答案
相关题目
15.已知函数y=f(x)满足f(1)=2,f′(1)=-1,则曲线g(x)=exf(x)在x=1处的切线斜率是( )
| A. | -e | B. | e | C. | 2e | D. | 3e |
19.已知正四面体ABCD,点E,F分别为棱AB,AC的中点,球O是正四面体ABCD的外接球,球O截直线EF所得的弦长为6$\sqrt{5}$,则正四面体的棱长为( )
| A. | 6$\sqrt{5}$ | B. | 12 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
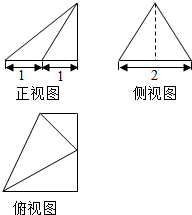 某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.
某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.