求下列函数的导函数:(1)y=e-x+25,-ln,(3)y=$\frac{\sqrt{2x-1}}{x}$．题目和参考答案——青夏教育精英家教网—

题目内容

14．求下列函数的导函数：
（1）y=e^-x+2（2x+1）⁵；
（2）y=cos（3x一1）-ln（-2x-1）；
（3）y=$\frac{\sqrt{2x-1}}{x}$．

分析根据复合函数的求导法则求导．

解答解：（1）y′=-e^-x+2（2x+1）⁵+10e^-x+2（2x+1）⁴；
（2）y′=-3sin（3x-1）-$\frac{2}{2x+1}$；
（3）y′=$\frac{x（2x-1）^{-\frac{1}{2}}-\sqrt{2x-1}}{{x}^{2}}$=$\frac{1}{x\sqrt{2x-1}}-\frac{\sqrt{2x-1}}{{x}^{2}}$．

点评本题考查了复合函数的导数，属于基础题．

练习册系列答案

同步解析与测评初中总复习指导与训练系列答案

5．若sinx=$\frac{3-2m}{2}$，x∈[-$\frac{π}{6}$，$\frac{5π}{6}$]，则m的取值范围是（　　）

2．已知在△ABC中，a，b，c分别为角A，B，C的对边，且$\frac{cosB}{cosC}$=$-\frac{b}{2a+c}$．
（1）求角B的大小；
（2）若b=4，求△ABC周长的最大值．

9．

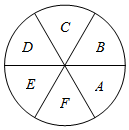如图所示，6个扇形区域A，B，C，D，E，F，现给这6个区域着色，要求同一个区域涂同一种颜色，相邻的两个区城不得使用同一种颜色，现有4种不同的颜色可用，那么一共有多少种不同的涂色方法？

19．已知{a_n}是等比数列，{b_n}是首项为1，公差d大于零的等差数列，且满足a₁b₁=3，a₂b₂=27，a₃b₃=135．
（1）求数列{a_n}，{b_n}的通项公式；
（2）求a₁b₁+a₂b₂+…+a_nb_n．

6．若复数$\frac{2a+2i}{1+i}$（α∈R）是纯虚数，则复数2a+2i在复平面内对应的点在（　　）

5．已知函数f（x）=$\frac{m}{x}$+lnx+x，g（x）=x³-3x．
（I）若m=2，求f（x）的极值；
（Ⅱ）若对于任意的s∈[$\frac{1}{2}$，2]，存在t∈[$\frac{1}{2}$，2]有f（s）≤g（t），求m的取值范围．

6．等差数列{a_n}的前n项和为S_n，若S₃=6，a₁=4，则S₅等于（　　）

试题分类