题目内容
18.已知过球面上三点A、B、C的截面到球心距离等于球半径的一半,且AC=BC=6,AB=4,则球面面积为( )| A. | 42π | B. | 48π | C. | 54π | D. | 60π |
分析 设出球的半径,小圆半径,通过已知条件求出两个半径,再求球的表面积.
解答 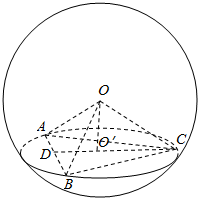 解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
则OO′⊥面ABC.在Rt△ACD中,cosA=$\frac{1}{3}$,则sinA=$\frac{2\sqrt{2}}{3}$.
在△ABC中,由正弦定理得$\frac{6}{sinA}$=2R,R=$\frac{9}{4}\sqrt{2}$,
△ABC外接圆的半径$r=\frac{{9\sqrt{2}}}{4}⇒{R^2}=\frac{27}{2}$,${S_{球表}}=4π{R^2}=54π$.
故选:C.
点评 本题考查立体几何中的球的切接和球的表面积问题,考查球面距离弦长问题,正弦定理的应用,考查学生分析问题解决问题能力,空间想象能力,属中等偏难题.

练习册系列答案
相关题目
9.已知$α∈(\frac{3π}{2},2π)$,sin(π+α)=$\frac{3}{5}$,则$sin(α+\frac{π}{2})$等于( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
3.已知$U=\{x|\frac{x-2}{x}≤1\}$,A={x|2-x≤1},则∁UA=( )
| A. | {x|x<1} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|x>1} |
10.函数f(x)=x2+mx+1的图象关于直线x=1对称,则( )
| A. | m=-2 | B. | m=2 | C. | m=-1 | D. | m=1 |