题目内容
20.已知函数y=Asin(ωx+φ)在一个周期内的图象如图所示,求其解析式.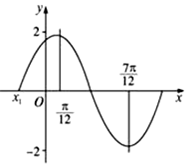
分析 要找y=Asin(ωx+φ)的解析式,从其图象可以看出:从$\frac{π}{12}$到$\frac{7π}{12}$是函数的半个周期,可求其周期是$\frac{1}{2}×$$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{12}$,即可求出ω=2,再从图象中可以看出振幅A=2,根据x=$\frac{π}{12}$时,y=2即可求得φ=$\frac{π}{3}$,从而得解.
解答 解:由函数图象可得:$\frac{1}{2}×$$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{12}$,
可求:ω=2,
又从图象中可以看出振幅A=2,
由于x=$\frac{π}{12}$时,y=2,
可得:2sin(2×$\frac{π}{12}$+φ)=2,由五点作图法可得:$\frac{π}{6}$+φ=$\frac{π}{2}$,
可求得φ=$\frac{π}{3}$,
可得函数解析式为:y=2sin(2x+$\frac{π}{3}$).
点评 本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,由五点法作图求出φ的值是解题的关键,属于基础题.

练习册系列答案
相关题目
10.函数f(x)=$\sqrt{3}$cos(x+2φ)是R上的奇函数,则φ可能是( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
9.《聪明花开》栏目共有五个项目,分别为“和一斗”、“斗麻利”、“文士生”、“讲头知尾”、“正功夫”.《聪明花开》栏目组为了解观众对项目的看法,设计了“你最喜欢的项目是哪一个”的调查问卷(每人只能选一个项目),对现场观众进行随机抽样调查,得到如下数据(单位:人):
(I)在所有参与该问卷调查的人中,用分层抽样的方法抽取n人座谈,其中恰有4人最喜欢“斗麻利”,求n的值及所抽取的人中最喜欢“合一斗”的人数;
(II)在(I)中抽取的最喜欢“合一斗”和“斗麻利”的人中,任选2人参加栏目组互动,求恰有1人最喜欢“合一斗”的概率.
| 合一斗 | 斗麻利 | 文士生 | 讲头知尾 | 正功夫 |
| 115 | 230 | 115 | 345 | 460 |
(II)在(I)中抽取的最喜欢“合一斗”和“斗麻利”的人中,任选2人参加栏目组互动,求恰有1人最喜欢“合一斗”的概率.
10.将函数y=sinx的图象的横坐标扩大3倍,再将图象向右平移3个单位,所得解析为( )
| A. | y=sin(3x+1) | B. | y=sin($\frac{1}{3}$x-1) | C. | y=sin(3x+3) | D. | y=sin($\frac{1}{3}$x-3) |