题目内容
方程sin(-πx)=
x的实数解的个数是 .
| 1 |
| 2014 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用,三角函数的图像与性质
分析:我们可以在同一个直角坐标系中分别画出y=sin(-πx)与函数y=
x的图象,然后分析他们交点的个数,进行得到方程sin(-πx)=
x的实数解的个数.
| 1 |
| 2014 |
| 1 |
| 2014 |
解答:
解:函数y=sin(-πx)与函数y=
x的图象如下图所示:
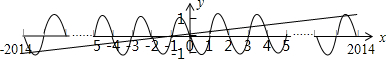
由图可得函数y=sin(-πx)的周期为2,
在每个区间(2k,2k+2)(k∈Z)上,y=sin(-πx)与函数y=
x的图象均有两个交点,
且两个函数图象还交于坐标原点,
故两个函数图象共有:
×2+1=4029个交点,
即方程sin(-πx)=
x有4029实数解
故答案为:4029
| 1 |
| 2014 |
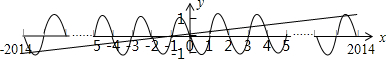
由图可得函数y=sin(-πx)的周期为2,
在每个区间(2k,2k+2)(k∈Z)上,y=sin(-πx)与函数y=
| 1 |
| 2014 |
且两个函数图象还交于坐标原点,
故两个函数图象共有:
| 2014-(-2014) |
| 2 |
即方程sin(-πx)=
| 1 |
| 2014 |
故答案为:4029
点评:本题考查的知识点是根的存在性及根的个数判断,判断方程实数根的个数,即判断对应函数零点的个数,这种转化思想是解答此类问题的关键.

练习册系列答案
相关题目
设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列命题,正确的是( )
| A、若m?β,α⊥β,则m⊥α |
| B、若m∥α,m⊥β,则α⊥β |
| C、若α⊥β,α⊥γ,则β⊥γ |
| D、若α∩γ=m,β∩γ=n,m∥n,则α∥β |