题目内容
17.已知P(x0,y0)是双曲线C:$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点,F1,F2是C的两个焦点,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$≥0,则x0的取值范围是( )| A. | [-$\frac{2\sqrt{6}}{3}$,$\frac{2\sqrt{6}}{3}$] | B. | (-$\frac{2\sqrt{6}}{3}$,$\frac{2\sqrt{6}}{3}$) | C. | (-∞,-$\frac{2\sqrt{6}}{3}$]∪[$\frac{2\sqrt{6}}{3}$,+∞) | D. | (-∞,-$\frac{2\sqrt{6}}{3}$)∪($\frac{2\sqrt{6}}{3}$,+∞) |
分析 求得双曲线的a,b,c,可得焦点坐标,运用向量的数量积的坐标表示,可得(-$\sqrt{3}$-x0)($\sqrt{3}$-x0)+y02≥0,再由点P满足双曲线的方程,化简整理,再由双曲线的范围,解不等式即可得到所求范围.
解答 解:双曲线C:$\frac{{x}^{2}}{2}-{y}^{2}$=1的a=$\sqrt{2}$,b=1,c=$\sqrt{3}$,
可得F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),
$\overrightarrow{P{F}_{1}}$=(-$\sqrt{3}$-x0,-y0),$\overrightarrow{P{F}_{2}}$=($\sqrt{3}$-x0,-y0),
$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$≥0,即为(-$\sqrt{3}$-x0)($\sqrt{3}$-x0)+y02≥0,
即有x02+y02-3≥0,
又P(x0,y0)是双曲线上一点,可得$\frac{{{x}_{0}}^{2}}{2}$-y02=1,
即有y02=$\frac{{{x}_{0}}^{2}}{2}$-1,
可得x02+$\frac{{{x}_{0}}^{2}}{2}$≥4,即有|x0|≥$\frac{2\sqrt{6}}{3}$,
由双曲线的性质可得|x0|≥$\sqrt{2}$,
即有x0≥$\frac{2\sqrt{6}}{3}$,或x0≤-$\frac{2\sqrt{6}}{3}$.
故选:C.
点评 本题考查双曲线的方程、性质和运用,考查向量的数量积的坐标表示,以及化简整理的运算能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.设数列{an}的前n项和为Sn,且a1=$\frac{1}{2}$,{Sn+nan}为常数列,则an=( )
| A. | $\frac{1}{n(n+1)}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{3}{(n+1)(n+2)}$ | D. | $\frac{5-2n}{6}$ |
8.在等差数列{an}中,a3+a6=a4+5,且a2不大于1,则a8的取值范围是( )
| A. | (-∞,9] | B. | [9,+∞) | C. | (-∞,9) | D. | (9,+∞) |
2.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点($\frac{a}{2}$,0)到直线l的距离d≥$\frac{1}{5}$c,则双曲线的离心率e的取值范围是( )
| A. | [$\frac{3}{2}$,2] | B. | [$\frac{\sqrt{5}}{2}$,2] | C. | [$\frac{3}{2}$,$\sqrt{5}$] | D. | [$\frac{\sqrt{5}}{2}$,$\sqrt{5}$] |
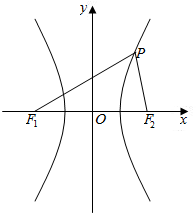 已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.
已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.