题目内容
7．函数f（x）=$\frac{1}{2}$arcsinx的定义域是[-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$]，求此函数的值域．分析 由条件利用反正弦函数的定义域和值域，求得此函数的值域．
解答 解：∵x∈[-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$]，∴arcsinx∈[-$\frac{π}{3}$，$\frac{π}{6}$]，∴函数f（x）=$\frac{1}{2}$arcsinx的值域为[-$\frac{π}{3}$，$\frac{π}{6}$]．
点评 本题主要考查反正弦函数的定义域和值域，属于基础题．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
17．已知P（x0，y0）是双曲线C：$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点，F1，F2是C的两个焦点，若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$≥0，则x0的取值范围是（ ）
| A． | [-$\frac{2\sqrt{6}}{3}$，$\frac{2\sqrt{6}}{3}$] | B． | （-$\frac{2\sqrt{6}}{3}$，$\frac{2\sqrt{6}}{3}$） | C． | （-∞，-$\frac{2\sqrt{6}}{3}$]∪[$\frac{2\sqrt{6}}{3}$，+∞） | D． | （-∞，-$\frac{2\sqrt{6}}{3}$）∪（$\frac{2\sqrt{6}}{3}$，+∞） |
15．
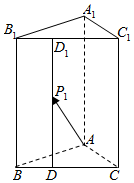如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=AC=$\sqrt{3}$，BC=3，AA1=5，$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$，$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$，$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$，一光线从A射出，第一次射到平面BCC1B1上点P1，经反射后第二次射到表面上点P2，依次下去，…，则P2P3=（ ）
如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=AC=$\sqrt{3}$，BC=3，AA1=5，$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$，$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$，$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$，一光线从A射出，第一次射到平面BCC1B1上点P1，经反射后第二次射到表面上点P2，依次下去，…，则P2P3=（ ）| A． | $\frac{\sqrt{10}}{6}$ | B． | $\frac{\sqrt{10}}{4}$ | C． | $\frac{\sqrt{10}}{3}$ | D． | $\frac{\sqrt{10}}{2}$ |