题目内容
6.求不等式(2x+1)2(x-3)(3x-2)3(x-4)≤0的解集.分析 第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0,(注意:一定要保证x前的系数为正数),第二步:将不等式号换成等号解出所有根,第三步:在数轴上从左到右依次标出各根,第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根”上去,一上一下依次穿过各根,第五步:观察不等号,如果不等号为“>”,则取数轴上方,穿根线以内的范围;如果不等号为“<”则取数轴下方,穿根线以内的范围,x的次数若为偶数则不穿过,即奇过偶不过.
解答 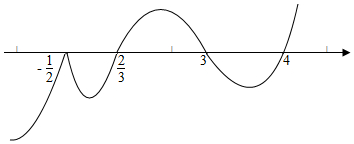 解:(2x+1)2(x-3)(3x-2)3(x-4)≤0,
解:(2x+1)2(x-3)(3x-2)3(x-4)≤0,
当(2x+1)2(x-3)(3x-2)3(x-4)=0,
解得x=-$\frac{1}{2}$或x=$\frac{2}{3}$,或x=3,或x=4,
将各根-$\frac{1}{2}$、$\frac{2}{3}$、3、4依次标在数轴上,
由图象可知不等式的解集为为(-∞,$\frac{2}{3}$]∪[3,4].
点评 本题考查了高次不等式的解法,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
17.已知P(x0,y0)是双曲线C:$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点,F1,F2是C的两个焦点,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$≥0,则x0的取值范围是( )
| A. | [-$\frac{2\sqrt{6}}{3}$,$\frac{2\sqrt{6}}{3}$] | B. | (-$\frac{2\sqrt{6}}{3}$,$\frac{2\sqrt{6}}{3}$) | C. | (-∞,-$\frac{2\sqrt{6}}{3}$]∪[$\frac{2\sqrt{6}}{3}$,+∞) | D. | (-∞,-$\frac{2\sqrt{6}}{3}$)∪($\frac{2\sqrt{6}}{3}$,+∞) |
11.已知向量|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,若向量$\overrightarrow{m}$满足|$\overrightarrow{m}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|$\overrightarrow{m}$|的最大值是( )
| A. | 2$\sqrt{3}$-1 | B. | 2$\sqrt{3}$+1 | C. | 4 | D. | $\sqrt{6}$+$\sqrt{2}$+1 |
15.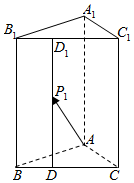 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )
 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=AC=$\sqrt{3}$,BC=3,AA1=5,$\overrightarrow{BD}$=$\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{{B}_{1}{D}_{1}}$=$\frac{1}{3}\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{D{P}_{1}}$=$\frac{3}{5}\overrightarrow{D{D}_{1}}$,一光线从A射出,第一次射到平面BCC1B1上点P1,经反射后第二次射到表面上点P2,依次下去,…,则P2P3=( )| A. | $\frac{\sqrt{10}}{6}$ | B. | $\frac{\sqrt{10}}{4}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{\sqrt{10}}{2}$ |
