题目内容
已知函数f(x)=
,g(x)=
,若函数h(x)=f(x)-g(x),则函数h(x)的零点的个数为( )
|
|
| A、2 | B、3 | C、4 | D、5 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由h(x)=f(x)-g(x)=0得数f(x)=g(x),分别作出函数f(x)和g(x)的图象,利用数形结合即可得到结论.
解答:
 解:由h(x)=f(x)-g(x)=0得数f(x)=g(x),
解:由h(x)=f(x)-g(x)=0得数f(x)=g(x),
∵数f(x)=
,g(x)=
,
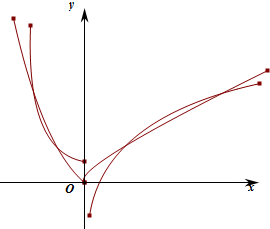
∴分别作出函数f(x)和g(x)的图象如图:
由图象可知两个函数图象有2个交点,即函数h(x)的零点的个数为4个,
故选:C
 解:由h(x)=f(x)-g(x)=0得数f(x)=g(x),
解:由h(x)=f(x)-g(x)=0得数f(x)=g(x),∵数f(x)=
|
|
∴分别作出函数f(x)和g(x)的图象如图:
由图象可知两个函数图象有2个交点,即函数h(x)的零点的个数为4个,
故选:C
点评:本题主要考查函数零点个数的判断,利用函数零点和函数图象之间的关系,利用数形结合是解决本题的关键.本题容易出错的地方在于作图不准确,错误A的比较多.

练习册系列答案
相关题目
计算sin780°的值为( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
阅读如图所示的语句,则语句的输出为s=( )


| A、25 | B、7 | C、13 | D、17 |
在△ABC中,已知向量
=(cos18°,cos72°),
=(2cos63°,2cos27°),则△ABC的最大内角为( )
| AB |
| BC |
| A、135° | B、120° |
| C、150° | D、90° |
函数y=cos2(2x-
)的最小正周期是( )
| π |
| 3 |
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
曲线y=sinx与x轴在区间[0,2π]上所围成阴影部分的面积为( )
| A、-4 | B、-2 | C、2 | D、4 |
已知点(
,2)在幂函数f(x)=xα(α>0)的图象上,则f(x)的表达式是( )
| 2 |
| A、f(x)=x2 | ||
| B、f(x)=x-2 | ||
C、f(x)=x
| ||
D、f(x)=x-
|