题目内容
设曲线C的参数方程为
(θ为参数),直线l的方程为x+y+1=0,则曲线C上到直线l距离为
的点的个数为( )
|
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点:直线的参数方程
专题:计算题,直线与圆,坐标系和参数方程
分析:将曲线C化为普通方程,得到圆(x+1)2+(y+2)2=8,圆心为(-1,-2),半径为2
,求出圆心到直线的距离,由图象即可得到答案.
| 2 |
解答:
 解:曲线C的参数方程为
解:曲线C的参数方程为
(θ为参数),
化为普通方程为圆(x+1)2+(y+2)2=8,
圆心为(-1,-2),半径为2
,
圆心到直线x+y+1=0的距离为d=
=
,
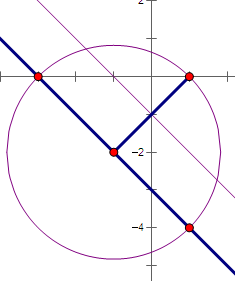
故由图形可知曲线C上到直线l距离为
的点的个数为3.
故选C.
 解:曲线C的参数方程为
解:曲线C的参数方程为
|
化为普通方程为圆(x+1)2+(y+2)2=8,
圆心为(-1,-2),半径为2
| 2 |
圆心到直线x+y+1=0的距离为d=
| |-1-2+1| | ||
|
| 2 |
故由图形可知曲线C上到直线l距离为
| 2 |
故选C.
点评:本题考查参数方程和普通方程的互化,考查直线与圆的位置关系,以及点到直线的距离公式,考查判断能力,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
已知f(x)=ax3+bx+1(ab≠0),若f(2012)=k,则f(-2012)=( )
| A、k | B、-k | C、1-k | D、2-k |
若点O是△ABC的外心,且
+
=
,则△ABC的内角C等于( )
| OA |
| OB |
| OC |
| A、45° | B、60° |
| C、90° | D、120° |
原命题“若a=0,则ab=0”,那么正确的是( )
| A、逆命题“若ab=0,则a=0”为真 |
| B、逆命题“若ab=0,则a=0”为假 |
| C、否命题“若a≠0,则ab≠0”为真 |
| D、逆否命题“若ab≠0,则a≠0”为假 |
函数y=x2lnx的导数是( )
| A、y′=2xlnx+x2 |
| B、y′=2xlnx-x2 |
| C、y′=2xlnx-x |
| D、y′=2xlnx+x |
 如图,在圆O中,AB是弦,AC是圆O切线,过B点作BD⊥AC于点D,BD交圆O于点E,若AE平分∠BAD,则∠ABD的度数是( )
如图,在圆O中,AB是弦,AC是圆O切线,过B点作BD⊥AC于点D,BD交圆O于点E,若AE平分∠BAD,则∠ABD的度数是( )| A、30° | B、45° |
| C、60° | D、50° |
设向量
与
的夹角为θ,
=(2,1),
+3
=(5,4),则sinθ=( )
| a |
| b |
| a |
| a |
| b |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|