题目内容
8.设△ABC的内角A、B、C的对边分别为a,b,c,且$\overrightarrow{u}$=(b,-$\sqrt{3}$a),$\overrightarrow{v}$=(sinA,cosB),$\overrightarrow{u}$⊥$\overrightarrow{v}$.(1)求角B的大小;
(2)若b=3,c=2a,求a,c的值.
分析 (1)利用$\overrightarrow{u}$⊥$\overrightarrow{v}$时$\overrightarrow{u}$•$\overrightarrow{v}$=0,列出等式,再利用正弦定理和同角的三角函数关系,求出B的值;
(2)根据余弦定理,结合题意列出方程组,即可求出a、c的值.
解答 解:(1)$\overrightarrow{u}$=(b,-$\sqrt{3}$a),$\overrightarrow{v}$=(sinA,cosB),且$\overrightarrow{u}$⊥$\overrightarrow{v}$,
∴$\overrightarrow{u}$•$\overrightarrow{v}$=bsinA-$\sqrt{3}$acosB=0,
即bsinA=$\sqrt{3}$acosB;
由正弦定理得sinBsinA=$\sqrt{3}$sinAcosB;
又A∈(0,π),∴sinA≠0,
∴sinB=$\sqrt{3}$cosB,
∴tanB=$\sqrt{3}$;
又B∈(0,π),∴B=$\frac{π}{3}$;
(2)由B=$\frac{π}{3}$,且b=3,c=2a,
根据余弦定理得b2=a2+c2-2accosB,
即32=a2+4a2-2a•2a•cos$\frac{π}{3}$,
解得a=$\sqrt{3}$或a=-$\sqrt{3}$(不合题意,舍去);
∴a=$\sqrt{3}$,c=2a=2$\sqrt{3}$.
点评 本题考查了正弦、余弦定理的应用问题,也考查了平面向量的数量积与同角三角函数关系的应用问题,是综合题.

练习册系列答案
相关题目
3.下面四个命题中的真命题是( )
| A. | 命题“?x≥2,均有x2-3x+2≥0”的否定是:“?x<2,使得x2-3x+2<0” | |
| B. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5、16、27、38、49的同学均被选出,则该班人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.3,则X在(0,2)内取值的概率为0.6 |
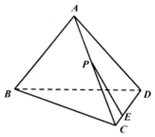 如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.
如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.