题目内容
定义在[-6，6]上的函数f（x）是增函数，则满足f（x）＜f（2x-3）的取值范围是 ．
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据函数的单调性和定义域建立不等式关系即可得到结论．
解答：
解：∵f（x）是定义在[-6，6]上的增函数，
∴由f（x）＜f（2x-3）得：
，
即
，
∴3＜x≤
，
故答案为：（3，
]．
∴由f（x）＜f（2x-3）得：
|
即
|
∴3＜x≤
| 9 |
| 4 |
故答案为：（3，
| 9 |
| 4 |
点评：本题主要考查函数单调性的应用，注意函数的定义域的限制．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
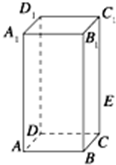如图，正四棱柱ABCD-A1B1C1D1中，AA1=2AB=4，点E在CC1上且C1E=3EC．试建立适当的坐标系，写出点B、C、E、A1的坐标．