题目内容
已知等差数列{an}的首项为a,公差为d,且方程ax2-3x+2=0的解为1和d,则数列{3n-1an}的前n项和Tn为( )
| A、3n |
| B、1+(n-1)3n |
| C、n•3n |
| D、1+(n+1)•3n |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:由已知条件推导出an=2n-1,从而得到3n-1an=(2n-1)•3n-1,由此利用错位相减法能求出数列{3n-1an}的前n项和Tn.
解答:
解:∵等差数列{an}的首项为a,公差为d,
且方程ax2-3x+2=0的解为1和d,
∴
,解得a=1,d=2,
∴an=2n-1a2=1+2=3,
∴3n-1an=(2n-1)•3n-1,
∴Tn=1×30+3×3+5×32+…+(2n-1)•3n-1.①
3Tn=1×3+3×32+5×33+…+(2n-1)×3n,②
①-②,得:-2Tn=1+2(3+32+33+…+3n-1)-(2n-1)•3n
=1+2×
-(2n-1)•3n
=-2-(2n-2)•3n,
∴Tn=1+(n-1)•3n.
故选:B.
且方程ax2-3x+2=0的解为1和d,
∴
|
∴an=2n-1a2=1+2=3,
∴3n-1an=(2n-1)•3n-1,
∴Tn=1×30+3×3+5×32+…+(2n-1)•3n-1.①
3Tn=1×3+3×32+5×33+…+(2n-1)×3n,②
①-②,得:-2Tn=1+2(3+32+33+…+3n-1)-(2n-1)•3n
=1+2×
| 3(1-3n-1) |
| 1-3 |
=-2-(2n-2)•3n,
∴Tn=1+(n-1)•3n.
故选:B.
点评:本题考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
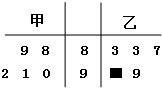 如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩,期中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为( )
如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩,期中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
若双曲线x2-
=1(b>0)的一条渐近线与圆x2+(y-2)2=1至多有一个交点,则双曲线离心率的取值范围是( )
| y2 |
| b2 |
| A、(1,2] | ||
| B、[2,+∞) | ||
C、(1,
| ||
D、[
|
先后抛掷红、蓝两枚骰子,事件A:红骰子出现3点,事件B:蓝骰子出现的点数为奇数,则P(A|B)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若关于x的不等式x2-x+a>0恒成立,则a的取值范围为( )
A、[
| ||
B、(
| ||
C、(-∞,
| ||
D、(-∞,
|
已知α为锐角,且sin(α-
)=
,则sinα=( )
| π |
| 4 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若执行如图所示的程序框图,当输入n=1,m=5,则输出p的值为( )


| A、-4 | B、1 | C、2 | D、5 |
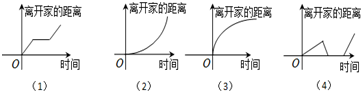
下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1)(2)(3)(4)时间时间时间时间离开家的距离离开家的距离离开家的距离离开家的距离

| A、(1)(2)(4) |
| B、(4)(2)(3) |
| C、(4)(1)(3) |
| D、(4)(1)(2) |