题目内容
5.到点(-4,0)与到直线x=-$\frac{25}{4}$的距离之比为$\frac{4}{5}$的动点的轨迹方程是$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.分析 先设动点的坐标,然后根据动点P到点(-4,0)与到直线x=-$\frac{25}{4}$的距离之比为$\frac{4}{5}$,列方程,整理即可求动点的轨迹方程.
解答 解:设动点的坐标为(x,y),
则由题意得$\frac{\sqrt{(x+4)^{2}+{y}^{2}}}{|x+\frac{25}{4}|}$=$\frac{4}{5}$,
整理得$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1,
所以动点的轨迹方程是$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.
故答案为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.
点评 本题主要考查直接法求轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
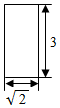
16.在正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1中,AB=AA1=2.若点M在△ABC所在平面上运动,且使得△AC1M的面积为1,则动点M的轨迹为( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |


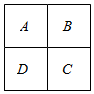 用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).
用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).