题目内容
17.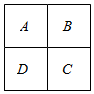 用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).
用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).(1)求恰好使用两种颜色完成涂色任务的概率;
(2)设甲、乙两人各自相互独立完成涂色任务,记他们所用颜色的种数差的绝对值为ξ,求ξ的分布列及数学期望E(ξ)
分析 (1)利用分类加法计数原理计算可知涂色方案共有260种,满足条件的方案由20种,利用概率计算公式计算即得结论;
(2)通过分别求出随机变量ξ可能取值为0,1,2时各自的概率,利用期望的定义计算即可.
解答 解:(1)由题意,涂色方式共三大类:
由分步计数原理可得,共${A}_{5}^{4}$+2×5×4×3+${A}_{5}^{2}$=260,
恰好使用两种颜色的方法有${A}_{5}^{2}$=20,
故所求概率P=$\frac{20}{260}$=$\frac{1}{13}$;
(2)依题意,随机变量ξ可能取值为0,1,2,
∵使用四种颜色的概率为$\frac{{A}_{5}^{4}}{260}$=$\frac{6}{13}$,使用三种颜色的概率为$\frac{2×5×4×3}{260}$=$\frac{6}{13}$,
∴P(ξ=0)=$\frac{1}{13}$×$\frac{1}{13}$+$\frac{6}{13}$×$\frac{6}{13}$+$\frac{6}{13}$×$\frac{6}{13}$=$\frac{73}{169}$,
P(ξ=1)=2($\frac{6}{13}$×$\frac{6}{13}$+$\frac{6}{13}$×$\frac{1}{13}$)=$\frac{84}{169}$,
P(ξ=2)=2×$\frac{6}{13}$×$\frac{1}{13}$=$\frac{12}{169}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{73}{169}$ | $\frac{84}{169}$ | $\frac{12}{169}$ |
点评 本题考查离散型随机变量的期望,涉及排列、组合等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
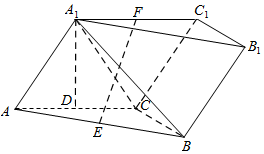 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.