题目内容
给出以下命题：
①对于平面几何中的命题：“夹在两条平行线之间的平行线段相等”，在立体几何中，类比上述命题，可以得到命题：“夹在两个平行平面间的平行线段相等”．
②
（2sinx+cosx）dx=2；
③已知函数f（x）=x3-3x的图象与直线y=a有相异三个公共点，则a的取值范围是（-2，2）
其中正确命题是（ ）
①对于平面几何中的命题：“夹在两条平行线之间的平行线段相等”，在立体几何中，类比上述命题，可以得到命题：“夹在两个平行平面间的平行线段相等”．
②
| ∫ |
0 |
③已知函数f（x）=x3-3x的图象与直线y=a有相异三个公共点，则a的取值范围是（-2，2）
其中正确命题是（ ）
| A、①②③ | B、①② | C、①③ | D、②③ |
考点：命题的真假判断与应用
专题：综合题
分析：①由类比推理的方法得出平面几何中的命题到立体几何中的命题，判定该命题正确；
②计算
（2sinx+cosx）dx的值，判定②错误；
③利用导数求出f（x）的极大值与极小值，结合图形，得出③正确．
②计算
| ∫ |
0 |
③利用导数求出f（x）的极大值与极小值，结合图形，得出③正确．
解答：
解：对于①，由平面几何中的命题“夹在两条平行线这间的平行线段相等”，
可以类比得出在立体几何中“夹在两个平行平面间的平行线段相等”，是一个真命题；∴①正确；
对于②，∵
（2sinx+cosx）dx=
2sinxdx+
cosxdx=-2cosx
+sinx
=-2（0-1）+（1-0）=3；∴②错误；
对于③，对f（x）求导，令f′（x）=3x2-3=0，得x=±1，求得f（x）的极大值为f（-1）=2，极小值为f（1）=-2，如图所示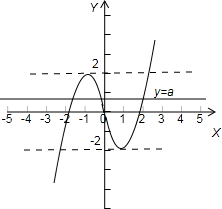
；
当满足-2＜a＜2时，恰有三个不同公共点；∴命题③正确．
综上，正确的命题是①③．
故选：C．
可以类比得出在立体几何中“夹在两个平行平面间的平行线段相等”，是一个真命题；∴①正确；
对于②，∵
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| | |
0 |
| | |
0 |
对于③，对f（x）求导，令f′（x）=3x2-3=0，得x=±1，求得f（x）的极大值为f（-1）=2，极小值为f（1）=-2，如图所示
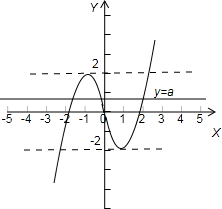；当满足-2＜a＜2时，恰有三个不同公共点；∴命题③正确．
综上，正确的命题是①③．
故选：C．
点评：本题通过命题真假的判定，考查了类比推理的应用问题，定积分的计算以及利用导数研究函数极值的问题，解题时应对每一个命题认真分析，以便作出正确的选择．
练习册系列答案
相关题目
下列说法错误的是（ ）
| A、如果命题“￢p”与命题“p∨q”都是真命题，那么命题q一定是真命题 | ||
| B、命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0” | ||
| C、若命题p：?x0∈R，x02+2x0-3＜0，则?p：?x∈R，x2+2x-3≥0 | ||
D、“sinθ=
|
已知直线y=b（b＞0）与曲线f（x）=sinx在y轴右侧依次的三个交点的横坐标x1，x2，x3成等比数列，则b的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
当x＞0，y＞0时，不等式
+
≤a
恒成立，则实数a的最小值是（ ）
| x |
| y |
| x+y |
A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
p：|a|≤1，q：函数f（x）=ax在R上单调递增，则￢p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
设P为曲线C：y=x2+2x+3上的点，且曲线C在点P处切线倾斜角的取值范围是（
，π），则点P横坐标的取值范围为（ ）
| 3π |
| 4 |
A、（-1，-
| ||
B、（-
| ||
| C、（0，1） | ||
D、（
|