题目内容
2. 如图,已知三棱锥A-OCB中,AO⊥底面BOC,且∠BAO=∠CAO=$\frac{π}{6}$,AB=4,点D为线段AB的中点,记二面角B-AO-C的大小为θ.
如图,已知三棱锥A-OCB中,AO⊥底面BOC,且∠BAO=∠CAO=$\frac{π}{6}$,AB=4,点D为线段AB的中点,记二面角B-AO-C的大小为θ.(1)求三棱锥A-OCB体积V的最大值;
(2)当$θ=\frac{2π}{3}$时,求二面角C-OD-B的余弦值.
分析 (1)由条件,∠BOC是二面角B-AO-C的平面角,即为θ,从而求出V=$\frac{4\sqrt{3}}{3}sinθ≤\frac{4\sqrt{3}}{3}$,由此求出当$θ=\frac{π}{2}$时,V取得最大值$\frac{4\sqrt{3}}{3}$.
(2)以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在直线为y轴,z轴,建立空间直角坐标系O-xyz,利用向量法能求出二面角C-OD-B的余弦值.
解答 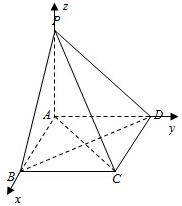 解:(1)由条件,∠BOC是二面角B-AO-C的平面角,即为θ,
解:(1)由条件,∠BOC是二面角B-AO-C的平面角,即为θ,
V=$\frac{1}{3}×\frac{1}{2}×BO×OC×sinθ×AO$=$\frac{4\sqrt{3}}{3}sinθ≤\frac{4\sqrt{3}}{3}$,
∴当$θ=\frac{π}{2}$时,V取得最大值$\frac{4\sqrt{3}}{3}$.
(2)如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在直线为y轴,z轴,
建立空间直角坐标系O-xyz,
则A(0,0,2$\sqrt{3}$),B(0,2,0),D(0,1,$\sqrt{3}$),C($\sqrt{3}$,-1,0),
设$\overrightarrow{n}$=(x,y,z)为平面COD的法向量,
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{OD}=y+\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{OC}=\sqrt{3}x-y=0}\end{array}\right.$,取z=$\frac{\sqrt{3}}{2}$,得$\overrightarrow{n}$=(-$\frac{\sqrt{3}}{2}$,-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
平面AOB的一个法向量$\overrightarrow{m}$=(1,0,0),
设二面角C-OD-B的平面角为θ,由图形知θ是钝角,
则cosθ=-$\frac{|\overrightarrow{n}•\overrightarrow{m}|}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=-$\frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{15}}{2}}$=-$\frac{\sqrt{5}}{5}$,
∴二面角C-OD-B的余弦值为-$\frac{\sqrt{5}}{5}$.
点评 本题考查三棱锥子的体积的最大值的求法,考查二面角的余弦值的求法,考查空间想象能力、运算求解能力,考查数形结合思想,是中档题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | a>c>b | B. | c>b>a | C. | c>a>b | D. | a>b>c |
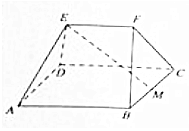 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.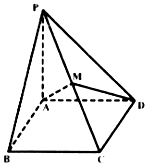 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.