题目内容
14.函数y=f(x)=$\frac{1}{3}$x3-x2+ax+a有三个零点,求a的取值范围.分析 作函数g(x)=-$\frac{1}{3}$x3+x2与y=ax+a的图象,从而设直线y=ax+a与函数g(x)=-$\frac{1}{3}$x3+x2相切于点(x1,y1),从而可得x1=0或x1=$\sqrt{3}$或x1=-$\sqrt{3}$;从而结合图象解得.
解答 解:作函数g(x)=-$\frac{1}{3}$x3+x2与y=ax+a的图象如下,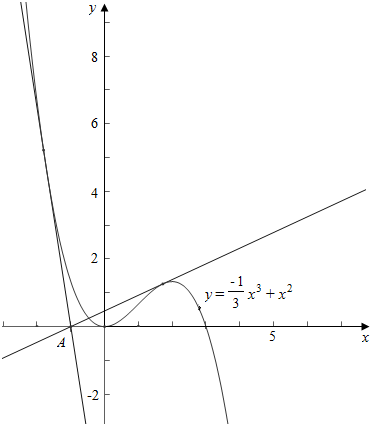
设直线y=ax+a与函数g(x)=-$\frac{1}{3}$x3+x2相切于点(x1,y1),
则$\frac{{y}_{1}-0}{{x}_{1}+1}$=-${{x}_{1}}^{2}$+2x1,且y1=-$\frac{1}{3}$x13+x12,
解得,x1=0或x1=$\sqrt{3}$或x1=-$\sqrt{3}$;
故-${{x}_{1}}^{2}$+2x1=0或2$\sqrt{3}$-3或-2$\sqrt{3}$-3;
结合图象可知,
a<-2$\sqrt{3}$-3或0<a<2$\sqrt{3}$-3.
点评 本题考查了导数的综合应用及数形结合的思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.函数f(x)=x3+3x2+3ax-4既有极大值又有极小值,则函数g(x)=x+$\frac{a}{x}$-2a在区间(1,+∞)上一定( )
| A. | 有最小值 | B. | 有最大值 | C. | 是减函数 | D. | 是增函数 |
2.不等式|3x+6|≤21的解集是( )
| A. | ∅ | B. | [-9,5] | C. | (-∞,-9)∪(5,+∞) | D. | R |
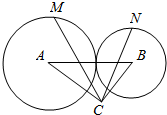 如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].
如图,圆A与圆B外切,半径分别为3,2,且△ABC是以C为直角顶点的Rt△.若AC=4.BC=3,点M,N分别在圆A,B上,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$,6+$\sqrt{145}$].