Question

6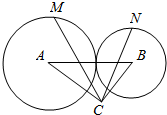．如图，圆A与圆B外切，半径分别为3，2，且△ABC是以C为直角顶点的Rt△．若AC=4．BC=3，点M，N分别在圆A，B上，则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$，6+$\sqrt{145}$]．

Answer 1

分析 以C为原点，CB所在直线为y轴，建立直角坐标系，即有圆A：（x-4）²+y²=9，圆B：x²+（y-3）²=4，设M（4+3cosα，3sinα），N（2cosβ，3+2sinβ），C（0，0），求得向量CM，CN的坐标，由向量的数量积的坐标表示，结合正弦、余弦函数的最值，即可得到所求范围．

解答 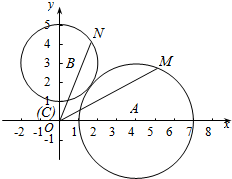解：以C为原点，CB所在直线为y轴，建立直角坐标系，
即有圆A：（x-4）²+y²=9，圆B：x²+（y-3）²=4，
设M（4+3cosα，3sinα），N（2cosβ，3+2sinβ），C（0，0），
则$\overrightarrow{CM}$=（4+3cosα，3sinα），$\overrightarrow{CN}$=（2cosβ，3+2sinβ），
$\overrightarrow{CM}$•$\overrightarrow{CN}$=（4+3cosα）•2cosβ+3sinα（3+2sinβ）
=6（cosαcosβ+sinαsinβ）+8cosβ+9sinα
=6cos（α-β）+8cosβ+9sinα，
当α=β+2kπ，k∈Z时，cos（α-β）取得最大为1，
8cosβ+9sinα=8cosα+9sinα=$\sqrt{145}$sin（α+θ），
当α+θ=2kπ+$\frac{π}{2}$，k∈Z时，取得最大，且为$\sqrt{145}$，
即有$\overrightarrow{CM}$•$\overrightarrow{CN}$的最大值为6+$\sqrt{145}$；
当β-α=2kπ+π，k∈Z，即有8cosβ+9sinα=8cos（2kπ+π+α）+9sinα
=9sinα-8cosα=$\sqrt{145}$sin（α-θ），
当α-θ=2kπ-$\frac{π}{2}$，k∈Z时，取得最小，且为-$\sqrt{145}$，
即有$\overrightarrow{CM}$•$\overrightarrow{CN}$的最小值为6-$\sqrt{145}$．
故答案为：[-6-$\sqrt{145}$，6+$\sqrt{145}$]．

点评 本题考查圆的参数方程的运用，考查向量的数量积的坐标表示，同时考查三角函数的性质的运用，属于中档题．