题目内容
如图，空间四边形ABCD中，E，F分别是AB，AD的中点，
G，H分别在BC，CD上，且BG∶GC＝DH∶HC＝1∶2.
(1)求证：E，F，G，H四点共面；
(2)设EG与FH交于点P，求证：P，A，C三点共线．
【证明】(1)∵E，F分别为AB，AD的中点，∴EF∥BD.
在△BCD中，
＝
＝
，∴GH∥BD，∴EF∥GH.
∴E，F，G，H四点共面．
(2)∵EG∩FH＝P，P∈EG，EG
平面ABC，
∴P∈平面ABC.同理P∈平面ADC.∴P为平面ABC与平面ADC的公共点．
又平面ABC∩平面ADC＝AC，∴P∈AC，∴P，A，C三点共线．
练习册系列答案
字词句段篇系列答案
相关题目
，则z=2x＋y－4的最大值为（ ）
，那么空白的判断框中应填人的条件是 （ ）
序号是( )
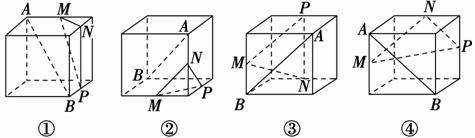
C．②③ D．②④