题目内容
15.在下列函数中,最小值为2的是( )| A. | y=2x+2-x | B. | y=sinx+$\frac{1}{sinx}$(0<x<$\frac{π}{2}$) | ||
| C. | y=x+$\frac{1}{x}$ | D. | y=log3x+$\frac{1}{lo{g}_{3}x}$(1<x<3) |
分析 根据题意,有基本不等式的性质依次分析4个选项函数的最小值,即可得答案.
解答 解:根据题意,依次分析选项:
对于A、y=2x+2-x=2x+$\frac{1}{{2}^{x}}$,而2x>0,则有y≥2,符合题意,
对于B、y=sinx+$\frac{1}{sinx}$,令t=sinx,0<x<$\frac{π}{2}$,则0<t<1,
有y>2,y=sinx+$\frac{1}{sinx}$没有最小值,不符合题意;
对于C、y=x+$\frac{1}{x}$,有x≠0,则有y≥2或y≤-2,不符合题意;
对于D、y=log3x+$\frac{1}{lo{g}_{3}x}$,令t=log3x,1<x<3,则有0<t<1,
有y>2,y=log3x+$\frac{1}{lo{g}_{3}x}$没有最小值,不符合题意;
故选:A.
点评 本题考查基本不等式的性质,注意基本不等式的使用条件.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
5.在锐角三角形△ABC中,a,b,c分别是角A,B,C的对边,(a+b+c)(a+c-b)=$({2+\sqrt{3}})ac$,则cosA+sinC的取值范围为( )
| A. | $({\frac{3}{2},\sqrt{3}})$ | B. | $({\frac{{\sqrt{3}}}{2},\frac{3}{2}})$ | C. | $({\frac{3}{2},\sqrt{3}}]$ | D. | $({\frac{{\sqrt{3}}}{2},\sqrt{3}})$ |
4.已知数列{an}满足:a1=-13,a6+a8=-2,且an-1=2an-an+1(n≥2),则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前13项和为( )
| A. | $\frac{1}{13}$ | B. | -$\frac{1}{13}$ | C. | $\frac{1}{11}$ | D. | -$\frac{1}{11}$ |
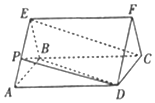 如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.
如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.