题目内容
1.曲线y=-ln(2x+1)+2在点(0,2)处的切线与直线y=0和y=2x围成的三角形的面积为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
分析 根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式,然后求出与y轴和直线y=2x的交点,根据三角形的面积公式求出所求即可.
解答 解:∵y=-ln(2x+1)+2,∴y'=-$\frac{2}{2x+1}$
∴y'|x=0=-2
∴曲线y=-ln(2x+1)+2在点(0,2)处的切线方程为y-2=-2(x-0)即2x+y-2=0
令y=0解得x=1,令y=2x解得x=$\frac{1}{2}$,y=1
∴切线与直线y=0和y=x围成的三角形的面积为$\frac{1}{2}$×1×1=$\frac{1}{2}$,
故选B.
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及两直线垂直的应用等有关问题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列函数中,其定义域和值域与函数y=elnx的定义域和值域相同的是( )
| A. | y=x | B. | y=lnx | C. | y=$\frac{1}{\sqrt{x}}$ | D. | y=10x |
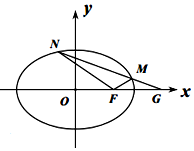 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,直线$\frac{{\sqrt{2}}}{2}x+y=1$经过E的右顶点和上顶点.
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,直线$\frac{{\sqrt{2}}}{2}x+y=1$经过E的右顶点和上顶点.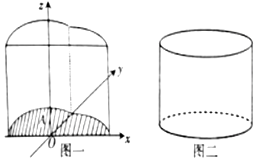 我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.
我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.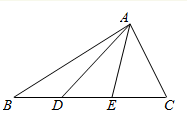 如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.
如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.