题目内容
9.实数x、y满足约束条件$\left\{\begin{array}{l}x+y≤4\\ x+2y≤6\\ x≥0\\ y≥0\end{array}\right.$,则目标函数k=2x+3y的最大值为10.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x+y≤4\\ x+2y≤6\\ x≥0\\ y≥0\end{array}\right.$作出可行域如图,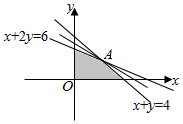
联立$\left\{\begin{array}{l}{x+2y=6}\\{x+y=4}\end{array}\right.$,解得A(2,2),
化目标函数k=2x+3y为$y=-\frac{2}{3}x+\frac{k}{3}$,
由图可知,当直线$y=-\frac{2}{3}x+\frac{k}{3}$过A时,直线在y轴上的截距最大,k有最大值为2×2+3×2=10.
故答案为:10.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
19.某地植被面积 x(公顷)与当地气温下降的度数y(℃)之间有如下的对应数据:
(1)请用最小二乘法求出y关于x的线性回归方程$\widehaty=\hat bx+\hat a$;
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少℃?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x(公顷) | 20 | 40 | 50 | 60 | 80 |
| y(℃) | 3 | 4 | 4 | 4 | 5 |
(2)根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少℃?
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
20.已知函数f(x)=(x+1)ln(x+1),若函数h(x)=2f(x-1)与y=x3-mx的图象在区间[$\frac{1}{e}$,e]上有2个不同的交点.则m的取值范围是( )
| A. | [1,2] | B. | (1,2+$\frac{1}{{e}^{2}}$] | C. | (1+$\frac{1}{e}$,3) | D. | (2,4+e] |
4.6名同学排成一排,则甲乙恰好相邻排在一起的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{6}$ |
18.已知$\overrightarrow{OA}$=(1,-2),$\overrightarrow{OB}$=(-3,1),则$\overrightarrow{AB}$=( )
| A. | (4,-3) | B. | (-4,3) | C. | (-2,-1) | D. | (2,1) |
19.甲、乙、丙三人站成一排站法的种数共有( )
| A. | 6 | B. | 3 | C. | 9 | D. | 12 |