题目内容
20.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B、C两点,过B作AC的垂线交x轴于点D,若点D到直线BC的距离小于a+$\sqrt{{a}^{2}+{b}^{2}}$,则$\frac{b}{a}$的取值范围为( )| A. | (0,1) | B. | (1,+∞) | C. | (0,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
分析 由双曲线的对称性知D在x轴上,设D(x,0),则由BD⊥AB得$\frac{{b}^{2}}{\frac{a}{c-x}}$•$\frac{{b}^{2}}{\frac{a}{c-x}}$=-1,求出c-x,利用D到直线BC的距离小于a+$\sqrt{{a}^{2}+{b}^{2}}$,即可得出结论.
解答 解:由题意,A(a,0),B(c,$\frac{{b}^{2}}{a}$),C(c,-$\frac{{b}^{2}}{a}$),由双曲线的对称性知D在x轴上,
设D(x,0),则由BD⊥AB得$\frac{{b}^{2}}{\frac{a}{c-x}}$•$\frac{{b}^{2}}{\frac{a}{c-x}}$=-1,
∴c-x=$\frac{{b}^{4}}{{a}^{2}(a-c)}$,
∵D到直线BC的距离小于a+$\sqrt{{a}^{2}+{b}^{2}}$,
∴c-x=|$\frac{{b}^{4}}{{a}^{2}(a-c)}$|<a+$\sqrt{{a}^{2}+{b}^{2}}$,
∴$\frac{{b}^{4}}{{a}^{2}}$<c2-a2=b2,
∴0<$\frac{b}{a}$<1,
故选:A.
点评 本题考查双曲线的性质,考查学生的计算能力,确定D到直线BC的距离是关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10.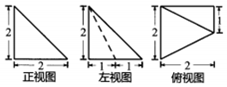 某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
 某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 3 |
8.已知复数z满足(1+i)z=1+3i(i是虚数单位),则z的共轭复数为( )
| A. | 1-i | B. | 1+i | C. | 2-i | D. | 2+i |
15.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F,作圆x2+y2=$\frac{{a}^{2}}{4}$的一条切线,切点为E,延长FE与双曲线的右支交于点P,若E是线段FP的中点,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
5.已知i为虚数单位,则$\frac{1+2i}{1-i}$的共轭复数为( )
| A. | -$\frac{1}{2}$+$\frac{3}{2}$i | B. | $\frac{1}{2}$+$\frac{3}{2}$i | C. | -$\frac{1}{2}$-$\frac{3}{2}$i | D. | $\frac{1}{2}$-$\frac{3}{2}$i |
12.已知三棱锥P-ABC的所有顶点都在表面积为16π的球O的球面上,AC为球O的直径,当三棱锥P-ABC的体积最大时,设二面角P-AB-C的大小为θ,则sinθ=( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{7}}{3}$ |
9.抛物线y2=4x的焦点为F,点A(3,2),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为( )
| A. | 4 | B. | 5 | C. | $4+2\sqrt{2}$ | D. | $5+\sqrt{5}$ |
10.设集合P={1,2,3,4},Q={x||x|≤3,x∈R},则P∩Q等于( )
| A. | {1} | B. | {1,2,3} | ||
| C. | {3,4} | D. | {-3,-2,-1,0,1,2,3} |