题目内容
18.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}x=\frac{1}{2}t\\ y=1-\frac{{\sqrt{3}}}{2}t\end{array}\right.$(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2sinθ.(Ⅰ)判断直线l与圆C的交点个数;
(Ⅱ)若圆C与直线l交于A,B两点,求线段AB的长度.
分析 (Ⅰ)直线l的参数方程消去参数t,能求出直线l的普通方程,圆C的极坐标方程为ρ=2sinθ,由ρ2=x2+y2,ρsinθ=y,能求出圆C的直角坐标方程,由此得到圆心(0,1)在直线l上,从而能求出直线l与圆C的交点个数.
(Ⅱ)由AB为圆C的直径,能求出|AB|的值.
解答 解:(Ⅰ)∵直线l的参数方程为$\left\{\begin{array}{l}x=\frac{1}{2}t\\ y=1-\frac{{\sqrt{3}}}{2}t\end{array}\right.$(t为参数).
∴消去参数t得直线l的普通方程为$\sqrt{3}x+y-1=0$,
∵圆C的极坐标方程为ρ=2sinθ,即ρ2=2ρsinθ,
∴由ρ2=x2+y2,ρsinθ=y,得圆C的直角坐标方程为x2+y2-2y=0.
∵圆心(0,1)在直线l上,
∴直线l与圆C的交点个数为2.
(Ⅱ)由(Ⅰ)知圆心(0,1)在直线l上,
∴AB为圆C的直径,
∵圆C的直角坐标方程为x2+y2-2y=0.
∴圆C的半径r=$\frac{1}{2}\sqrt{4}$=1,∴圆C的直径为2,∴|AB|=2.
点评 本题考查直线与圆的交点个数的判断,考查弦长的求法,是基础题,解题时要认真审题,注意参数方程、直角坐标方程、极坐标方程的互化公式的合理运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{kx+3,x≥0}\\{(\frac{1}{2})^{x},x<0}\end{array}\right.$,若方程f(f(x))-2=0恰有三个实数根,则实数k的取值范围是( )
| A. | [0,+∞) | B. | [1,3] | C. | (-1,-$\frac{1}{3}$] | D. | [-1,-$\frac{1}{3}$] |
13. 中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )
中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )
 中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )
中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)( )| A. | 2000 | B. | 2800 | C. | 3000 | D. | 6000 |
3.曲线y=x${\;}^{\frac{1}{2}}$与y=x2所围成的封闭区域的面积为( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{12}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{2}$ |
10.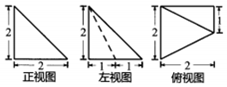 某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
 某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 3 |
8.已知复数z满足(1+i)z=1+3i(i是虚数单位),则z的共轭复数为( )
| A. | 1-i | B. | 1+i | C. | 2-i | D. | 2+i |