题目内容
 在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.(1)证明:AE∥平面BCD;
(2)证明:平面BDE⊥平面CDE;
(3)求该几何体的体积.
考点:组合几何体的面积、体积问题,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取BC的中点M,连接DM、AM,由等腰三角形三线合一,可得DM⊥BC,进而由平面BCD⊥平面ABC,结合面面垂直的性质定理可得DM⊥平面ABC,再由AE⊥平面ABC,结合线面垂直的性质定理,可得AE∥DM,进而由线面平行的判定定理得到AE∥平面BCD;
(2)由(1)知AE∥DM,AE=DM,可由平行四边形的性质得DE∥AM,再由(1)得DM⊥AM,结合线面垂直的判定定理可得AM⊥平面BCD,即DE⊥平面BCD,进而DE⊥CD,再由BD⊥CD结合线面垂直的判定定理和面面垂直的判定定理得到平面BDE⊥平面CDE;
(3)先证出BC⊥平面AEDM,即BC为组合体高之和,求出平面AEDM的面积,代入棱锥体积公式可得答案.
(2)由(1)知AE∥DM,AE=DM,可由平行四边形的性质得DE∥AM,再由(1)得DM⊥AM,结合线面垂直的判定定理可得AM⊥平面BCD,即DE⊥平面BCD,进而DE⊥CD,再由BD⊥CD结合线面垂直的判定定理和面面垂直的判定定理得到平面BDE⊥平面CDE;
(3)先证出BC⊥平面AEDM,即BC为组合体高之和,求出平面AEDM的面积,代入棱锥体积公式可得答案.
解答:
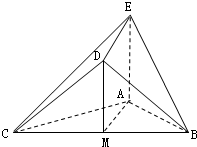 证明:(1)取BC的中点M,连接DM、AM,由已知BD=CD,可得:DM⊥BC,
证明:(1)取BC的中点M,连接DM、AM,由已知BD=CD,可得:DM⊥BC,
又因为平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,
所以DM⊥平面ABC,
因为AE⊥平面ABC,所以AE∥DM,
又因为AE?平面BCD,DM?平面BCD,
所以AE∥平面BCD.(4分)
(2)由(1)知AE∥DM,又AE=1,CM=1,
所以四边形DMAE是平行四边形,则有DE∥AM,
由(1)得DM⊥AM,又AM⊥BC,
∴AM⊥平面BCD,所以DE⊥平面BCD,
又CD?平面BCD,所以DE⊥CD,
由已知BD⊥CD,DE∩BD=D,
∴CD⊥平面BDE,
因为CD?平面CDE,
所以平面BDE⊥平面CDE.(10分)
(也可利用勾股定理等证明题中的垂直关系)
解:(3)∵BC⊥DM,BC⊥AM,DM∩AM=M,
∴BC⊥平面AEDM,(11分)
AM=
,DM=1,
易得四边形AEDM为矩形其面积S=
,(12分)
故该几何体的体积V=VC-AEDM+VB-AEDM=
×S×BC=
.(14分)
 证明:(1)取BC的中点M,连接DM、AM,由已知BD=CD,可得:DM⊥BC,
证明:(1)取BC的中点M,连接DM、AM,由已知BD=CD,可得:DM⊥BC,又因为平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,
所以DM⊥平面ABC,
因为AE⊥平面ABC,所以AE∥DM,
又因为AE?平面BCD,DM?平面BCD,
所以AE∥平面BCD.(4分)
(2)由(1)知AE∥DM,又AE=1,CM=1,
所以四边形DMAE是平行四边形,则有DE∥AM,
由(1)得DM⊥AM,又AM⊥BC,
∴AM⊥平面BCD,所以DE⊥平面BCD,
又CD?平面BCD,所以DE⊥CD,
由已知BD⊥CD,DE∩BD=D,
∴CD⊥平面BDE,
因为CD?平面CDE,
所以平面BDE⊥平面CDE.(10分)
(也可利用勾股定理等证明题中的垂直关系)
解:(3)∵BC⊥DM,BC⊥AM,DM∩AM=M,
∴BC⊥平面AEDM,(11分)
AM=
| 3 |
易得四边形AEDM为矩形其面积S=
| 3 |
故该几何体的体积V=VC-AEDM+VB-AEDM=
| 1 |
| 3 |
2
| ||
| 3 |
点评:本题考查的知识点是组合几何体的体积问题,直线与平面平行的判定,平面与平面垂直的判定,是空间线面关系的缩应用,难度中档.

练习册系列答案
相关题目
已知点 A(2,-3),B(-3,-2),若直线l:y=k(x-1)+1与线段AB相交,则直线l的斜率的范围是( )
A、k≥
| ||
B、-4≤k≤
| ||
C、k<-
| ||
D、-
|
定义在R上的函数f(x)=e|x|+x
,且f(x+t)>f(x)在x∈(-1,+∞)上恒成立,则关于x的方程f(x)=f(t)-e的根的个数叙述正确的是( )
| 4 |
| 3 |
| A、有两个 | B、有一个 |
| C、没有 | D、上述情况都有可能 |