题目内容
5.若异面直线a,b所成角为60°,AB是公垂线,E,F分别是异面直线a,b上到A,B距离为2,1的两点,当|EF|=3时,线段AB的长为$\sqrt{2}$或$\sqrt{6}$.分析 由$\overrightarrow{EF}$=$\overrightarrow{EA}$+$\overrightarrow{AB}$+$\overrightarrow{BF}$,两边平方即可解得线段AB的长.
解答 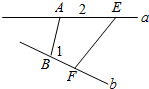 解:如图,由$\overrightarrow{EF}$=$\overrightarrow{EA}$+$\overrightarrow{AB}$+$\overrightarrow{BF}$,得
解:如图,由$\overrightarrow{EF}$=$\overrightarrow{EA}$+$\overrightarrow{AB}$+$\overrightarrow{BF}$,得
由$\overrightarrow{EF}$2=$\overrightarrow{EA}$2+$\overrightarrow{AB}$2+$\overrightarrow{BF}$2+2|$\overrightarrow{EA}$||$\overrightarrow{BF}$|cosθ
①当θ=60°时,有9=4+$\overrightarrow{AB}$2+1+2•2•$\frac{1}{2}$,得|$\overrightarrow{AB}$|=$\sqrt{2}$;
②当θ=120°时,有9=4+$\overrightarrow{AB}$2+1-2•2•$\frac{1}{2}$,得|$\overrightarrow{AB}$|=$\sqrt{6}$.
∴线段AB的长为$\sqrt{2}$或$\sqrt{6}$.
故答案为:$\sqrt{2}$或$\sqrt{6}$.
点评 本题考虑到若用前两种方法都难以奏效,于是选用了“回路法”,更方便了“异面直线a,b所成的角为60°”的讨论与运用,使得解题快捷无比.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
12.已知$\overrightarrow{a}$=(-2,3),$\overrightarrow{b}$=(3,1),则2$\overrightarrow{a}$+$\overrightarrow{b}$和$\overrightarrow{a}$-$\overrightarrow{b}$的坐标分别为( )
| A. | (-1,7),(5,2) | B. | (-1,7),(-5,2) | C. | (1,4),(5,2) | D. | (-1,4),(-5,2) |
13.在△ABC中,cos(A+B)=( )
| A. | cosC | B. | -cosC | C. | sinC | D. | -sinC |
15.已知椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中:
(1)求椭圆C1和抛物线C2的标准方程;
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点.
①求证:直线PA,PF,PB的斜率成等差数列;
②若点P在x轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点.
①求证:直线PA,PF,PB的斜率成等差数列;
②若点P在x轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
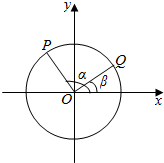 如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求:
如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求: 四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,
四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,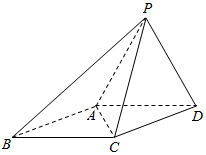 如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.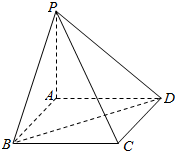 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.