题目内容
2.已知点E是正方形ABCD的边AD上一动点(端点除外),现将△ABE沿BE所在直线翻折成△A′BE,并连结A′C,A′D.记二面角A′-BE-C的大小为α(0<α<π).则( )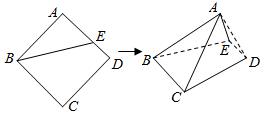
| A. | 存在α,使得BA′⊥面A′DE | B. | 存在α,使得BA′⊥面A′CD | ||
| C. | 存在α,使得EA′⊥面A′CD | D. | 存在α,使得EA′⊥面A′BC |
分析 Rt△ABE绕BE旋转的几何体是两个圆锥的组合体,能推导出某个位置存在母线A′E⊥AE,即A′E⊥BC,从而得到存在α,使得EA′⊥面A′BC.
解答  解:作AF⊥BE于F,交DC于G,则当折叠时,A′的投影在FG上
解:作AF⊥BE于F,交DC于G,则当折叠时,A′的投影在FG上
设正方形的边长为1,则A′B=1,BD=$\sqrt{2}$,
∵A′E+ED=1>A′D,
∴∠BA′D≠90°,故A和B错误;
∵二面角A′-BE-C的大小为α(0<α<π),不存在母线EA′⊥A′C,
∴不可能存在α,使得EA′⊥面A′CD,故C错误;
Rt△ABE绕BE旋转的几何体是两个圆锥的组合体,
∵∠A′BE<45°,45°<∠A′EB<90°,
∴某个位置存在母线A′E⊥AE,即A′E⊥BC,
∵二面角A′-BE-C的大小为α(0<α<π),
∴存在α,使得EA′⊥面A′BC,故D正确.
故选:D.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
11.若函数f(x)满足f′(x)-f(x)=2xex,f(0)=1,其中f′(x)为f(x)的导函数,则当x>0时,$\frac{f′(x)}{f(x)}$的最大值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
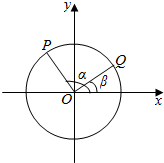 如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求:
如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求: 四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,
四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,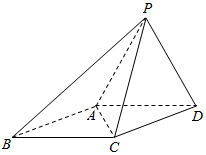 如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形. 如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.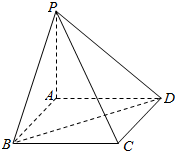 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.