题目内容
4．在△ABC中，角A、B、C的对边分别是a，b，c，已知2acosA=-$\sqrt{3}$（ccosB+bcosC）．（1）求角A；
（2）若b=2，且△ABC的面积为$\frac{\sqrt{3}}{2}$，求a的值．
分析 （1）根据正弦定理和两角和得正弦公式和诱导公式可得，
（2）先由三角形的面积公式求出c，再根据余弦定理即可求出．
解答 解：（1）∵2acosA=-$\sqrt{3}$（ccosB+bcosC）
由正弦定理可得2sinAcosA=-$\sqrt{3}$（sinCcosB+sinBcosC）=-$\sqrt{3}$sin（B+C）=-$\sqrt{3}$sinA，
∵sinA≠0，
∴cosA=-$\frac{\sqrt{3}}{2}$，
∴A=$\frac{5π}{6}$
（2）b=2，且△ABC的面积为$\frac{\sqrt{3}}{2}$，
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×2×$\frac{1}{2}$c=$\frac{\sqrt{3}}{2}$，
解得c=$\sqrt{3}$，
由余弦定理可得a2=b2+c2-2bccosA=4+3-2×2×$\sqrt{3}$×（-$\frac{\sqrt{3}}{2}$）=13，
则a=$\sqrt{13}$
点评 本题考查三角函数的化简，正弦定理、余弦定理和三角形的面积公式应用等知识，属于中档题．
练习册系列答案
相关题目
如图所示的数阵中，用A（m，n）表示第m行的第n个数，则以此规律A（8，2）为$\frac{1}{122}$．
某三棱锥的三视图如图所示，则该三棱锥最长的棱为3．
9．
某多面体的三视图如图所示，则该多面体的体积为（ ）
某多面体的三视图如图所示，则该多面体的体积为（ ）| A． | 2 | B． | $\frac{20}{3}$ | C． | $\frac{22}{3}$ | D． | 4 |
16．从一批苹果中，随机抽取65个，其重量（克）的数据分布表如下：
（1）用分层抽样的方法从重量在[80，85）和[95，100）的品种共抽取4个，重量在[80，85）的有几个？
（2）在（1）中抽取4个苹果中任取2个，其重量在[80，85）和[95，100）中各有1个的概率．
| 分组（重量） | [80，85） | [85，90） | [90，95） | [95，100） |
| 频数（个） | 5 | 15 | 30 | 15 |
（2）在（1）中抽取4个苹果中任取2个，其重量在[80，85）和[95，100）中各有1个的概率．
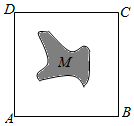如图，面积为S的正方形ABCD中有一个不规则的图形M，可以用随机模拟方法近似计算M的面积，在正方向ABCD中随机投掷3600个点，若恰好有1200个点落入M中，则M的面积的近似值为$\frac{S}{3}$．