题目内容
20.已知G点为△ABC的重心,设△ABC的内角A,B,C的对边分别为a,b,c且满足$\overrightarrow{BG}$⊥$\overrightarrow{CG}$,若$\frac{a^2}{cosA}=λbc$则实数λ=$\frac{1}{2}$.分析 如图,连接AG,延长交AG交BC于D,由于G为重心,故D为中点,CG⊥BG,可得DG=$\frac{1}{2}$BC,由重心的性质得,AD=3DG,即AD=$\frac{3}{2}$BC,利用余弦定理可得:AC2+AB2=2BD2+2CD2,即b2+c2=5a2,由$\frac{a^2}{cosA}=λbc$,可得λ=$\frac{2{a}^{2}}{{b}^{2}+{c}^{2}-{a}^{2}}$.
解答 解:如图,连接AG,延长交AG交BC于D,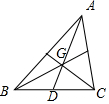
由于G为重心,故D为中点,
∵CG⊥BG,∴DG=$\frac{1}{2}$BC,
由重心的性质得,AD=3DG,即AD=$\frac{3}{2}$BC,
由余弦定理得,AC2=AD2+CD2-2AD•CD•cos∠ADC,
AB2=AD2+BD2-2AD•BDcos∠ADB,
∵∠ADC+∠BDC=π,CD=BD,
∴AC2+AB2=2BD2+2AD2,
∴AC2+AB2=$\frac{1}{2}$BC2+$\frac{9}{2}$BC2=5BC2,
∴b2+c2=5a2,
∵$\frac{a^2}{cosA}=λbc$,∴λ=$\frac{2{a}^{2}}{{b}^{2}+{c}^{2}-{a}^{2}}$=$\frac{2{a}^{2}}{5{a}^{2}-{a}^{2}}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了余弦定理、三角形重心性质、中线长定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10..已知O是坐标原点,点A(1,0),若点M(x,y)为平面区域$\left\{\begin{array}{l}x+y≥2\\ x≤1\\ y≤2\end{array}\right.$上的一个动点,则$|{\overrightarrow{OA}+\overrightarrow{OM}}|$的最大值是( )
| A. | $\sqrt{5}$ | B. | 1 | C. | $2\sqrt{2}$ | D. | $\frac{1}{2}$ |