题目内容
15.在棱长为1的正方体ABCD-A'B'C'D'中,异面直线A'D与AB'所成角的大小是$\frac{π}{3}$.分析 根据题意,连接B′C,得出∠AB′C是异面直线A'D与AB'所成的角,利用等边三角形求出它的大小.
解答 解:正方体ABCD-A'B'C'D'中,
连接A′D、AB′、B′C,如图所示;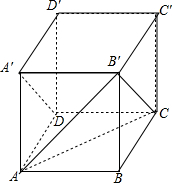
则A′B′∥DC,且A′B′=DC,
∴四边形A′B′CD是平行四边形,
∴A′D∥B′C,
∴∠AB′C是异面直线A'D与AB'所成的角,
连接AC,则△AB′C是边长为$\sqrt{2}$等边三角形,
∴∠AB′C=$\frac{π}{3}$,
即异面直线A'D与AB'所成角是$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了空间中两条异面直线所成角的作法与计算问题,是基础题.

练习册系列答案
相关题目
6.已知双曲线$\frac{x^2}{9}-\frac{y^2}{16}$=1的左右焦点分别为F1,F2,若双曲线上一点P 满足∠F1PF2=90°,求${S_{△{F_1}P{F_2}}}$=16.
4.已知函数f(x)=$\frac{\sqrt{|x|}}{{e}^{x}}$(x∈R),若关于x的方程f2(x)-$\frac{1}{2}$mf(x)+$\frac{1}{2}$m-1=0恰好有4个不相等的实根,则m的取值范围是( )
| A. | (2,$\frac{\sqrt{2e}}{e}$+2) | B. | (1,$\frac{\sqrt{2e}}{e}$+1) | C. | (1,$\frac{\sqrt{2e}}{2e}$+1) | D. | (2,$\frac{\sqrt{2e}}{2e}$+2) |
9.已知命题p:?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0,命题q:实数x,y∈R,若x+y>2,则x>1或y>1;若p∧q为假命题,则( )
| A. | 函数f(x)为R上增函数 | B. | 函数f(x)为R上减函数 | ||
| C. | 函数f(x)在R上单调性不确定 | D. | 命题q为假命题 |
 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).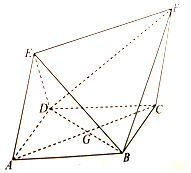 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.