题目内容
下列命题中,假命题是( )
A、若a,b∈R且a+b=1,则a•b≤
| ||||||
B、若a,b∈R,则
| ||||||
C、
| ||||||
| D、?x0,y0∈R,x02+y02+x0y0<0 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.a,b∈R且a+b=1,考虑a,b>0时,利用基本不等式可得1≥2
;
B.a,b∈R,由a2+b2≥2ab,可得2(a2+b2)≥(a+b)2,即可得出
≥(
)2≥ab;
C.变形利用基本不等式
=
+
≥2
,即可;
D.由于x02+y02+x0y0=(x0+
y0)2+
>0.即可判断出.
| ab |
B.a,b∈R,由a2+b2≥2ab,可得2(a2+b2)≥(a+b)2,即可得出
| a2+b2 |
| 2 |
| a+b |
| 2 |
C.变形利用基本不等式
| x2+3 | ||
|
| x2+1 |
| 2 | ||
|
| 2 |
D.由于x02+y02+x0y0=(x0+
| 1 |
| 2 |
| 3 |
| 4 |
| y | 2 0 |
解答:
解:A.a,b∈R且a+b=1,考虑a,b>0时,1≥2
,则a•b≤
正确;
B.a,b∈R,∵a2+b2≥2ab,∴2(a2+b2)≥(a+b)2,则
≥(
)2≥ab恒成立;
C.
=
+
≥2
,当且仅当x2=1时取等号,因此
(x∈R) 的最小值是2
,正确;
D.x02+y02+x0y0=(x0+
y0)2+
≥0.∴不?x0,y0∈R,使得x02+y02+x0y0<0成立.
综上可知:只有D是假命题.
故选;D.
| ab |
| 1 |
| 4 |
B.a,b∈R,∵a2+b2≥2ab,∴2(a2+b2)≥(a+b)2,则
| a2+b2 |
| 2 |
| a+b |
| 2 |
C.
| x2+3 | ||
|
| x2+1 |
| 2 | ||
|
| 2 |
| x2+3 | ||
|
| 2 |
D.x02+y02+x0y0=(x0+
| 1 |
| 2 |
| 3 |
| 4 |
| y | 2 0 |
综上可知:只有D是假命题.
故选;D.
点评:本题考查了基本不等式的应用,属于基础题.

练习册系列答案
相关题目
一个平面将一个半径为2的实心球截为两个部分,且截面经过球心,那么每个部分的表面积为( )
| A、12π | B、16π |
| C、4π | D、8π |
用数学归纳法证明2n>n2(n∈N*,n≥5)成立时,第二步归纳假设正确写法( )
| A、假设n=k时命题成立 |
| B、假设n=k(k∈N*)时命题成立 |
| C、假设n=k(n≥5)时命题成立 |
| D、假设n=k(n>5)时命题成立 |
若函数f(x)=
(a,b,c,d∈R)的图象如图所示,则a:b:c:d=( )
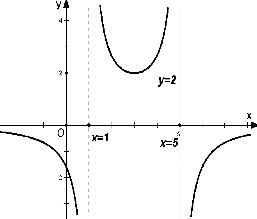
| d |
| ax2+bx+c |

| A、1:6:5:8 |
| B、1:6:5:(-8) |
| C、1:(-6):5:8 |
| D、1:(-6):5:(-8) |
独立性检验,适用于检查( )变量之间的关系.
| A、线性 | B、非线性 |
| C、解释与预报 | D、分类 |