题目内容
16.三棱柱ABC-A1B1C1的侧棱与底面垂直,且所有棱长均相等,M为A1C1的中点,则直线CM和直线A1B所成角的余弦值为( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{9}{10}$ |
分析 根据题意画出图形,结合图形找出异面直线CM与A1B所成的角,再求该角的余弦值.
解答 解:如图所示,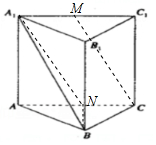
三棱柱ABC-A1B1C1中,侧棱与底面垂直,所有棱长均相等,
取AC的中点N,连接A1N,
∵M为A1C1的中点,
∴MC∥A1N,
∴∠BA1N是直线CM与A1B所成的角,
设三棱柱的棱长为2,
则A1B=2$\sqrt{2}$,A1N=$\sqrt{5}$,BN=$\sqrt{3}$,
且BN⊥平面ACC1A1,
∴BN⊥A1N,
∴直线CM和直线A1B所成角的余弦值为
cos∠BA1N=$\frac{{A}_{1}N}{{A}_{1}B}$=$\frac{\sqrt{5}}{2\sqrt{2}}$=$\frac{\sqrt{10}}{4}$.
故选:B.
点评 本题考查了空间想象力以及异面直线所成角的计算问题,是综合性题目.

练习册系列答案
相关题目
4.一圆的面积以10πcm2/s速度增加,那么当圆半径r=20cm时,其半径r的增加速率u为( )
| A. | $\frac{1}{2}$cm/s | B. | $\frac{1}{3}$cm/s | C. | $\frac{1}{4}$cm/s | D. | $\frac{1}{5}$cm/s |
11.下列四个结论中正确的个数为( )
①两条不同的直线都和同一个平面平行,则这两条直线平行.
②两条不同直线都和第三条直线垂直,则这两条直线平行.
③若a∥α,b⊆α,则a∥b
④若a∥b,b⊆α,则a∥α
①两条不同的直线都和同一个平面平行,则这两条直线平行.
②两条不同直线都和第三条直线垂直,则这两条直线平行.
③若a∥α,b⊆α,则a∥b
④若a∥b,b⊆α,则a∥α
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.一块边长为6cm的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为( )
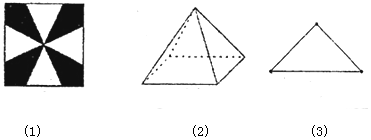

| A. | $12\sqrt{6}c{m^3}$ | B. | $4\sqrt{6}c{m^3}$ | C. | $27\sqrt{2}c{m^3}$ | D. | $9\sqrt{2}c{m^3}$ |
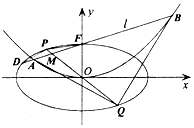 在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.
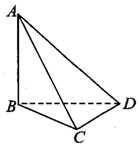
在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.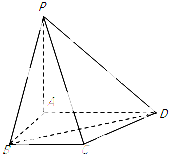 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.