��Ŀ����
10�������������տ�������ָ����С��Ϊ�ߵ����弶�������Ӧ�����������߸����ָ��Խ��˵����Ⱦ�����Խ���أ�������Σ��Խ��| ָ�� | ���� | ��� | �������� |
| 0��50 | �� | �� | ������� |
| 51��100 | �� | �� | |
| 101��150 | �� | ����Ⱦ | ����Ⱥ֢״����ȼӾ磬������Ⱥ���ִ̼�֢״�����ಡ�ͺ���ϵͳ��������Ӧ����������ĺͻ����� |
| 151��200 | �����Ⱦ | ||
| 201��250 | �� | �ж���Ⱦ | ���ಡ�ͷβ�����֢״�����Ӿ磬�˶����������ͣ�������Ⱥ���ձ����֢״�������˺����ಡ���β�����Ӧ����������� |
| 251��300 | �ж�����Ⱦ | ||
| 301��500 | �� | ����Ⱦ | �������˶����������ͣ�������ǿ��֢״����ǰ����ijЩ�����������˺Ͳ���Ӧ���������ڣ������������ģ�һ����ȺӦ�������ٻ����� |
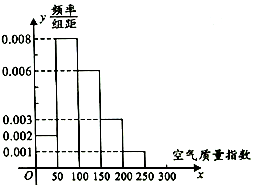
��1������60�����������Ⱦ��������
��2������60���������ָ����ƽ��ֵ��
��3����Ƶ�ʷֲ�ֱ��ͼ�е������������������Ϊ��һ�飬�ڶ��飬���������飮�ӵ�һ��͵������е����������г�����죬�����ǵĿ�������ָ���ֱ�Ϊx��y�����¼�|x-y|��150�ĸ��ʣ�
���� ��1����2������Ƶ�ʷֲ�ֱ��ͼ�����㼴�ɣ�
��3�������9���г��2���һ�п��ܽ���Ļ����¼���36�֣���|x-y|��150֪����ֻ����ͬһ���У���������ͬһ���еĻ����¼���18�֣��Ӷ�������������ĸ��ʼ��ɣ�
��� �⣺��1��������֪�������Ⱦ����������ָ����151��200֮�䣬����0.003��50��60=9�죮
��2����ֱ��ͼ֪60���������ָ����ƽ��ֵΪ$\overline x=25��0.1+75��0.4+125��0.3+175��0.15+225��0.05=107.5$��
��3����һ��͵�����������ֱ�Ϊ60��0.1=6�죬60��0.05=3�죬
���9���г��2���һ�п��ܽ���Ļ����¼���36�֣�
��|x-y|��150֪����ֻ����ͬһ���У���������ͬһ���еĻ����¼���18�֣�
��M��ʾ|x-y|��150��һ�¼��������$P��M��=\frac{18}{36}=\frac{1}{2}$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬Ҳ������������¼��ĸ��ʵļ������⣬���е��⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
18��������[-1��4]�����ѡȡһ����x����x��1�ĸ���Ϊ��������
| A�� | $\frac{2}{5}$ | B�� | $\frac{3}{5}$ | C�� | $\frac{1}{5}$ | D�� | $\frac{2}{3}$ |
5����x0Ϊ����f��x��=sin��x����㣬������$|{x_0}|+f��{x_0}+\frac{1}{2}����11$��������������У�������
| A�� | 18�� | B�� | 19�� | C�� | 20�� | D�� | 21�� |
2����֪��p��x��y������$\left\{\begin{array}{l}x+y-2\sqrt{2}��0\\ x��2\sqrt{2}\\ y��2\sqrt{2}\end{array}\right.$����p��x��y����Բx2+y2=1���������ߣ��е�ֱ��ǵ�A�͵�B����APB���ʱ��$\overrightarrow{PA}•\overrightarrow{PB}$��ֵ�ǣ�������
| A�� | 2 | B�� | 3 | C�� | $\frac{5}{2}$ | D�� | $\frac{3}{2}$ |
19����f'��x���Ǻ���f��x�������ڣ�0��+�ޣ��ϵĵ�����������$xf'��x��+2f��x��=\frac{1}{x^2}$�������в���ʽһ���������ǣ�������
| A�� | $\frac{f��e��}{e^2}��\frac{{f��{e^2}��}}{e}$ | B�� | $\frac{f��2��}{9}��\frac{f��3��}{4}$ | C�� | $\frac{f��2��}{e^2}��\frac{f��e��}{4}$ | D�� | $\frac{f��e��}{e^2}��\frac{f��3��}{9}$ |
13���Ȳ�����{an}��ǰn���ΪSn��������d��0����S8-S5����S9-S5����0��������
| A�� | |a7|��|a8| | B�� | |a7|��|a8| | C�� | |a7|=|a8| | D�� | |a7|=0 |