题目内容

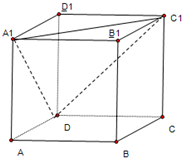在正方体ABCD-A1B1C1D1中，求平面A1DC1与平面ADD1A1所成角的正切值．
考点：与二面角有关的立体几何综合题
专题：计算题,空间角
分析：连接AD1，AD1∩A1D=O，连接C1O，可得∠C1OD1为平面A1DC1与平面ADD1A1所成角的平面角，从而可求平面A1DC1与平面ADD1A1所成角的正切值．
解答： 解：连接AD1，AD1∩A1D=O，则AD1⊥A1D，
连接C1O，则C1O⊥A1D，
∴∠C1OD1为平面A1DC1与平面ADD1A1所成角的平面角，
设正方体的棱长为2，则OD1=
2
，
∴tan∠C1OD1=
C1D1
OD1
=
2
2
=
2
点评：本题考查面面角，考查学生的计算能力，正确作出面面角是关键．
练习册系列答案
相关题目
已知二次函数f（x）=ax2+bx+c，（a，b，c∈R）的最小值为-1，且关于x的一元二次不等式ax2+bx+c＞0的解集为（-∞，-2）∪（0，+∞）．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）设F（x）=tf（x）-x-3其中t≥0，求函数F（x）在x∈[-
3
2
，2]时的最大值H（t）
（Ⅲ）若g（x）=f（x）+k（k为实数），对任意m∈[0，+∞），总存在n∈[0，+∞）使得g（m）=H（n）成立，求实数k的取值范围．
已知函数f(x)=lnx-
a
x

（1）若a＞0，试判断f（x）在定义域内的单调性；
（2）若f（x）＜x2在（1，+∞）上恒成立，求a的取值范围．
若不等式|x|＜1成立，则不等式[x-（a+1）][x-（a+4）]＜0也成立，求实数a的取值范围．
如图，边长为2的菱形ABCD中，∠ABC=60°，点E，F分别是AB，BC的中点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′．

（1）求证：A′D⊥EF；
（2）求二面角A′-EF-D的余弦值．
如图1，在平面直角坐标系中，拋物线y=ax2+c与x轴正半轴交于点F（4，0）、与y轴正半轴交于点E（0，4），边长为4的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合；
（1）求拋物线的函数表达式；
（2）如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线与边AB交于点P且同时与边CD交于点Q．设点A的坐标为（m，n）
①当PO=PF时，分别求出点P和点Q的坐标及PF所在直线l的函数解析式；
②当n=2时，若P为AB边中点，请求出m的值；
（3）若点B在第（2）①中的PF所在直线l上运动，且正方形ABCD与抛物线有两个交点，请直接写出m的取值范围．
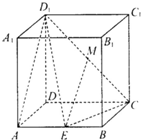在长方体ABCD-A1B1C1D1中，AD=1，AA1=AB=2．点E是线段AB上的动点，点M为D1C的中点．
（1）当E点是AB中点时，求证：直线ME∥平面ADD1A1；
（2）若二面角A-D1E-C的余弦值为
4
5
15
．求线段AE的长．
如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，∠ABC=
π
4
，PA⊥底面ABCD，PA=2，M为PA的中点，N为BC的中点．AF⊥CD于F，如图建立空间直角坐标系．
（Ⅰ）求出平面PCD的一个法向量并证明MN∥平面PCD；
（Ⅱ）求二面角P-CD-A的余弦值．
一弹簧在弹性限度内，拉伸弹簧所用的力与弹簧伸长的长度成正比．如果20N的力能使弹簧伸长3cm，则把弹簧从平衡位置拉长6cm（在弹性限度内）时所做的功为
 
．（单位：焦耳）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网