题目内容
已知椭圆中心在原点,焦点在x轴上,长轴长等于12,离心率为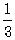 .
.
(Ⅰ)求椭圆的标准方程;
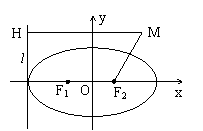
(Ⅱ)过椭圆左顶点作直线l,若动点M到椭圆右焦点的距离比它到直线l的距离小4,求 点M的轨迹方程.
点M的轨迹方程.
 【解】(Ⅰ)设椭圆的半长轴长为a,半短轴长为b,半焦距为c.
【解】(Ⅰ)设椭圆的半长轴长为a,半短轴长为b,半焦距为c.
由已知,2a=12,所以a=6. 又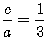 ,即a=3c,所以3c=6,即c=2.
,即a=3c,所以3c=6,即c=2.
于是b2=a2-c2=36-4=32.
因为椭圆的焦点在x轴上,故椭圆的标准方程是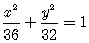 .
.
(Ⅱ)法一:因为a=6,所以直线l的方程为x=-6,又c=2,所以右焦点为F2(2,0).
过点M作直线l的垂线,垂足为H,由题设,|MF2|=|MH|-4.
设点M(x,y),则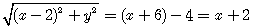 .
.
两边平方,得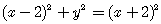 ,即y2=8x. 故点M的轨迹方程是y2=8x.
,即y2=8x. 故点M的轨迹方程是y2=8x.
法二:因为a=6,c=2,所以a-c=4,从而椭圆 左焦点F1到直线l的距离为4.
左焦点F1到直线l的距离为4.
由题设,动点M到椭圆右焦点的距离与它到直线x=-2的距离相等,所以点M的轨迹是以右焦点为F2(2,0)为焦点,直线x=-2为准线的抛物线.
显然抛物线的顶点在坐标原点,且p= |F1F2|=4,故点M的轨迹方程是y2=8x
|F1F2|=4,故点M的轨迹方程是y2=8x

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 作垂直于实轴
作垂直于实轴 的直线,交双曲线于P、Q,
的直线,交双曲线于P、Q, 是另一焦点,若∠
是另一焦点,若∠ ,则双曲线的离心率
,则双曲线的离心率 等于( )
等于( )
 B
B C
C D
D
 上的函数
上的函数 ,对任意
,对任意 ,都有
,都有 成立,若函数
成立,若函数 的图象关于点
的图象关于点 对称,则
对称,则 =( )
=( )
 只有一个公共点的直线有( )
只有一个公共点的直线有( ) 且
且 组成等差数列(n为正偶数),又
组成等差数列(n为正偶数),又
 ;
; 与3的大小,并说明理由.
与3的大小,并说明理由.