题目内容
4.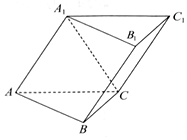 已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.
已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.(1)求侧棱A1A与底面ABC所成角的大小;
(2)求四棱锥C-AA1B1B的体积.
分析 (1)如图所示,取AC的中点O,连接A1O,B1C.AA1=A1C,可得A1O⊥AC.根据二面角A1-AC-B是直二面角,
可得平面AA1C1C⊥平面ABC.于是A1O⊥平面ABC.可得∠A1AO为侧棱A1A与底面ABC所成角.根据等腰直角三角形的性质即可得出:侧棱A1A与底面ABC所成角.
(2)△ABC中,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,可得AB=2$\sqrt{2}$.S△ABC=$\frac{1}{2}AB×BC$.四棱锥C-AA1B1B的体积=${V}_{{A}_{1}{B}_{1}{C}_{1}-ABC}$-${V}_{C-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{2}{3}{S}_{△ABC}×{A}_{1}O$,即可得出.
解答 解:(1)如图所示,取AC的中点O,连接A1O,B1C.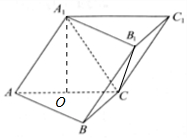
∵AA1=A1C,∴A1O⊥AC.
∵二面角A1-AC-B是直二面角,
∴平面AA1C1C⊥平面ABC.平面AA1C1C∩平面ABC=AC.
∴A1O⊥平面ABC.
∴∠A1AO为侧棱A1A与底面ABC所成角.
∵AA1⊥A1C,AA1=A1C.
∴∠A1AC=45°,A1O=AO=$\sqrt{3}$.
即侧棱A1A与底面ABC所成角为45°.
(2)△ABC中,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,
∴AB=$\sqrt{(2\sqrt{3})^{2}-{2}^{2}}$=2$\sqrt{2}$.
∴S△ABC=$\frac{1}{2}AB×BC$=$\frac{1}{2}×2\sqrt{2}×2$=2$\sqrt{2}$.
∴四棱锥C-AA1B1B的体积=${V}_{{A}_{1}{B}_{1}{C}_{1}-ABC}$-${V}_{C-{A}_{1}{B}_{1}{C}_{1}}$
=$\frac{2}{3}{S}_{△ABC}×{A}_{1}O$
=$\frac{2}{3}×2\sqrt{2}×$$\sqrt{3}$=$\frac{4\sqrt{6}}{3}$.
点评 本题考查了空间位置关系、空间角、等腰直角三角形的性质、勾股定理、三棱柱与三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程R(公里) | ||
| 100≤R<180 | 180≤R<280 | <280 | |
| 纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
| 分组 | 频数 | 频率 |
| 100≤R<180 | 3 | 0.3 |
| 180≤R<280 | 6 | x |
| R≥280 | y | z |
| 合计 | M | 1 |
(2)若从这M辆纯电动乘用车任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为X(单位:万元),求X的分布列和数学期望值E(X).
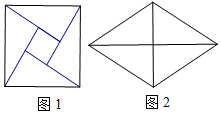 中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )
中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )| A. | $\frac{24}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{25}$ |
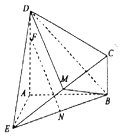 如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥
如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥